2023-2024学年四川省成都市锦江区嘉祥外国语高级中学高三（上）入学数学试卷（理科）

一．选择题（共12小题）

• 1．已知全集U=A∪B={x∈Z|0≤x≤6}，A∩（∁_UB）={1，3，5}，则B=（　　）

  A．{2，4，6}

  B．{1，3，5}

  C．{0，2，4，6}

  D．{x∈Z|0≤x≤6}
  组卷：321引用：5难度：0.9

  解析

• 2．已知复数z满足z=

  2

  i

  1

  +

  i

  ，那么z的共轭复数在复平面上对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：139引用：11难度：0.9

  解析

• 3．在等差数列{a_n}中，a₂=3，a₆=11，直线l过点M（m,a_m），N（n,a_n）（m≠n,m,n∈N^*），则直线l的斜率为（　　）

  A．2

  B．-2

  C．4

  D．-4
  组卷：165引用：6难度：0.8

  解析

• 4．直线

  x

  -

  3

  y

  =

  0

  绕原点按顺时针方向旋转30°后所得的直线l与圆（x-2）²+y²=3的位置关系是（　　）

  A．直线l过圆心

  B．直线l与圆相交，但不过圆心

  C．直线l与圆相切

  D．直线l与圆无公共点
  组卷：176引用：4难度：0.8

  解析

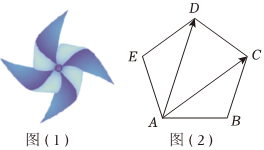• 5．剪（折）纸是幼儿园大班儿童的必修课，通过剪（折）纸，可以培养儿童的动手能力和热爱劳动的优秀品质以及对艺术作品的欣赏能力．通过对正三角形、正方形、正五边形、正六边形纸片进行简单的裁剪、折叠可以制作出三叶风车、四叶风车、五叶风车、六叶风车．如图（1）是一个五叶风车，图（2）是正五边形ABCDE，若该正五边形的边长为1，则

  AC

  •

  AD

  =（　　）

  A． 2 cos 2 π 5

  B．2cos3 π 5

  C． 4 cos 2 π 5

  D．4cos3 π 5
  组卷：29引用：2难度：0.6

  解析

• 6．如图，某同学用两根木条钉成十字架，制成一个椭圆仪．木条中间挖一道槽，在另一活动木条PAB的P处钻一个小孔，可以容纳笔尖，A，B各在一条槽内移动，可以放松移动以保证PA与PB的长度不变，当A，B各在一条槽内移动时，P处笔尖就画出一个椭圆E．已知|PA|=2|AB|，且P在右顶点时，B恰好在O点，则E的离心率为（　　）

  A． 1 2

  B． 2 3

  C． 2 5 5

  D． 5 3
  组卷：138引用：5难度：0.6

  解析

• 7．奇函数f（x）在R上存在导数f'（x），当x＜0时，f'（x）＜-

  2

  x

  f（x），则使得（x²-1）f（x）＜0成立的x的取值范围为（　　）

  A．（-1，0）∪（0，1）	B．（-∞，-1）∪（0，1）
  C．（-1，0）∪（1，+∞）	D．（-∞，-1）∪（1，+∞）
  组卷：802引用：7难度：0.3

  解析

三，解答题。（70分，17题10分，其余每题12分）

• 21．随着互联网的兴起，越来越多的人选择网上购物．某购物平台为了吸引顾客提升销售额，每年双十一都会进行某种商品的促销活动，该商品促销活动规则如下：①“价由客定”，即所有参与该商品促销活动的人进行网络报价，每个人并不知晓其他人的报价也不知道参与该商品促销活动的总人数；②报价时间截止后，系统根据当年双十一该商品数量配额，按照参与该商品促销活动人员的报价从高到低分配名额；③每人限购一件，且参与人员分配到名额时必须购买，某位顾客拟参加2019年双十一该商品促销活动，他为了预测该商品最低成交价，根据该购物平台的公告统计了最近5年双十一参与该商品促销活动的人数（见表）：
  

  年份	2014	2015	2016	2017	2018
  年份编号t	1	2	3	4	5
  参与人数y（百万人）	0.5	0.6	1	1.4	1.7

  （1）由收集数据的散点图发现，可用线性回归模拟拟合参与人数y（百万人）与年份编号t之间的相关关系．请用最小二乘法求y关于t的线性回归方程：

  ̂

  y

  =

  ̂

  b

  t+

  ̂

  a

  ，并预测2019年双十一参与该商品促销活动的人数；
  （2）该购物平台调研部门对2000位拟参与2019年双十一该商品促销活动人员的报价价格进行了一个抽样调查，得到如下的一份频数表：
  

  报价区间（千元）	[1，2）	[2，3）	[3，4）	[4，5）	[5，6）	[6，7）
  频数	200	600	600	300	200	100

  ①求这200位参与人员报价X的平均值

  x

  和样本方差s²（同一区间的报价可用该价格区间的中点值代替）；
  ②假设所有参与该商品促销活动人员的报价X可视为服从正态分布N（μ，σ²）且μ与σ²可分别由①中所求的样本平均值

  x

  和样本方差s²估值，若预计2019年双十一该商品最终销售量为317400，请你合理预测（需说明理由）该商品的最低成交价．
  参考公式及数据（i）回归方程：

  ̂

  y

  =

  ̂

  b

  t+

  ̂

  a

  ，其中

  ̂

  b

  =

  n

  ∑

  i

  =

  1

  x

  i

  y

  i

  -

  n

  x

  y

  n

  ∑

  i

  =

  1

  x

  i

  2

  -

  n

  x

  2

  ，

  ̂

  a

  =

  y

  -

  ̂

  b

  x.
  （ii）

  5

  ∑

  i

  =

  1

  t

  2

  1

  =55，

  5

  ∑

  i

  =

  1

  t

  i

  y

  i

  =18.8，

  1

  .

  7

  ≈1.3；
  （iii）若随机变量Z服从正态分布N（μ，σ²），则P（μ-σ＜Z＜μ+σ）=0.6826，P（μ-2σ＜Z＜μ+2σ）=0.9544，P（μ-3σ＜Z＜μ+3σ）=0.9974．
  组卷：125引用：2难度：0.6

  解析

• 22．如图，设椭圆C：

  x

  2

  a

  2

  +y²=1（a＞1）．
  （Ⅰ）求直线y=kx+1被椭圆截得到的弦长（用a,k表示）
  （Ⅱ）若任意以点A（0，1）为圆心的圆与椭圆至多有三个公共点，求椭圆的离心率的取值范围．
  组卷：5730引用：5难度：0.1

  解析