2023年广东省东莞市光明中学中考数学一模试卷

一、选择题（每题3分，共30分）

• 1．下列四个数中，属于无理数的是（　　）

  A．0

  B． 22 7

  C．π

  D．（-2）-1
  组卷：120引用：1难度：0.9

  解析

• 2．2023年全国一半公共预算教育支出安排超4.2万亿元．政府工作报告中提到，5年来，财政性教育经费占国内生产总值比例每年都保持在4%以上，学生人均经费投入大幅增加，其中4.2万亿用科学记数法表示是（　　）

  A．4.2×1013

  B．4.2×1012

  C．4.2×1011

  D．4.2×103
  组卷：42引用：1难度：0.8

  解析

• 3．下列运算正确的是（　　）

  A．2 3 - 3 =2	B．（a+1）2=a2+1
  C．（a2）3=a5	D．2a2•a=2a3
  组卷：1104引用：21难度：0.7

  解析

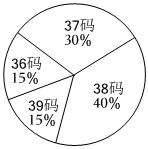• 4．如图是一家鞋店在一段时间内销售了某种女鞋各种尺码的销售情况统计图，则所销售的女鞋尺码的众数是（　　）

  A．36

  B．37

  C．38

  D．39
  组卷：108引用：1难度：0.7

  解析

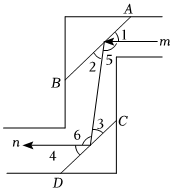• 5．如图是小亮绘制的潜望镜原理示意图，两个平面镜的镜面AB与CD平行，入射光线m与出射光线n平行．若入射光线m与镜面AB的夹角∠1=40°，则∠6的度数为（　　）

  A．100°

  B．90°

  C．80°

  D．70°
  组卷：257引用：5难度：0.6

  解析

• 6．不等式组

  3 （ x - 2 ） ≤ x - 4

  3 x ＞ 2 x - 1

  的解集在数轴上表示正确的是（　　）

  A．	B．
  C．	D．
  组卷：1349引用：23难度：0.6

  解析

• 7．下列命题中，是真命题的是（　　）

  A．太阳光线下形成的投影是中心投影

  B．反比例函数y= 1 x 的图象既是轴对称图形又是中心对称图形

  C．对角线相等的四边形是矩形

  D．若a＞b,则3-a＞3-b
  组卷：54引用：1难度：0.7

  解析

• 8．数学小组研究如下问题：东莞市地处北纬约23°的纬度上，求北纬23°纬线的长度，小组成员查阅相关资料，得到如下信息：
  
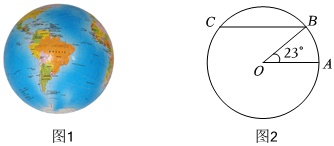
  信息一：如图1，在地球仪上，与赤道平行的圆圈叫做纬线；
  信息二：如图2，赤道半径OA约为6400千米，弦BC∥OA，以BC为直径的圆的周长就是北纬23°纬线的长度；（参考数据：π≈3.14，sin23°≈0.39，cos23°≈0.92，tan23°≈0.42）
  根据以上信息，北纬23纬线的长度约是（　　）

  A．5900千米

  B．16000千米

  C．37000千米

  D．42000千米
  组卷：138引用：1难度：0.5

  解析

五、解答题（三）（每题10分，共20分）；

• 24．【问题探究】（1）如图（1）在正方形ABCD中，AB=6，点E为DC上的点，DE=2CE，连接BE，点O为BE上的点，过点O作MN⊥BE交AD于点M，交BC于点N，则MN的长度为

  ；
  【类比迁移】（2）如图（2）在矩形ABCD中，AB=6，BC=8，连接BD，过BD的中点O作MN⊥BD交AD于点M，交BC于点N，求MN的长度．
  【拓展应用】（3）如图（3）李大爷家有一块平行四边形ABCD的菜地，测得AB=

  5

  2

  米，BC=7米，∠ABC=45°，为了管理方便，李大爷沿着对角线BD开一条小路，过这小路的正中间，开了另一条垂直于它的小路MN（小路面积忽略不计），求新开出的小路MN的长度．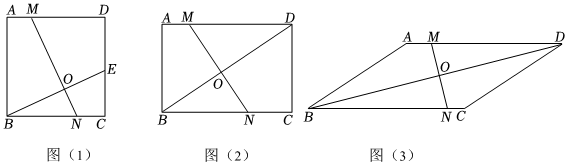
  
  组卷：183引用：3难度：0.3

  解析

• 25．如图，已知抛物线y=ax²+bx+c（a≠0）的图象与x轴交于点A（-1，0）和点B（3，0），与y轴交于点C（0，-3）．
  （1）求二次函数的表达式；
  （2）如图，点M是直线BC下方的二次函数图象上的一个动点，过点M作MH⊥x轴于点H，交BC于点N，求线段MN最大时点M的坐标；
  （3）在（2）的条件下，该抛物线上是否存在点Q，使得∠QCB=∠CBM．若存在，请直接写出点Q的坐标；若不存在，请说明理由．
  
  组卷：943引用：5难度：0.5

  解析