2023-2024学年甘肃省兰州市城关区树人中学九年级（上）第一次月考数学试卷
发布：2024/9/14 0:0:8
一、选择题（每小题3分，共36分）
-
1．
的倒数是（ ）-12023组卷：1378引用：50难度：0.9 -
2．中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录，下列四幅作品分别代表“立春”、“谷雨”、“白露”、“大雪”，其中是中心对称图形的是（ ）
组卷：2175引用：74难度：0.9 -
3．如图，已知AB∥CD∥EF，BC：CE=3：4，AF=21，那么DF的长为（ ）组卷：135引用：1难度：0.7 -
4．不等式-3（x+1）＞-6的解集表示在数轴上正确的是（ ）
组卷：427引用：7难度：0.7 -
5．用配方法解方程x2+8x+7=0，则配方正确的是（ ）
组卷：5849引用：188难度：0.9 -
6．方程
的解是（ ）3xx-1=2+1x-1组卷：281引用：3难度：0.5 -
7．根据下列表格的对应值：
由此可判断方程x2+12x-15=0必有一个根满足（ ）x 1 1.1 1.2 1.3 x2+12x-15 -2 -0.59 0.84 2.29 组卷：2517引用：34难度：0.5 -
8．端午节又称端阳节，是中华民族重要的传统节日，我国各地都有吃粽子的习俗．某超市以10元每袋的价格购进一批粽子，根据市场调查，售价定为每袋16元，每天可售出200袋；若售价每降低1元，则可多售出80袋，问此种粽子售价降低多少元时，超市每天售出此种粽子的利润可达到1440元？若设每袋粽子售价降低x元，则可列方程为（ ）
组卷：794引用：10难度：0.8 -
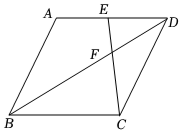9．如图，在边长为4的菱形ABCD中，E为AD边的中点，连接CE交对角线BD于点F．若∠DEF=∠DFE，则这个菱形的面积为（ ）组卷：3042引用：17难度：0.6
三、解答题（共12小题，共72分）
-
27．点P、点P′和点Q为平面直角坐标系中的三个点，给出如下定义：若PQ=P′Q，且∠PQP′=90°，则称P′为点P关于点Q的等垂点．
（1）已知点Q的坐标为（4，0），
①如图1，若点P为原点，直接写出P关于Q的等垂点P′的坐标 ；
②如图2，P为y轴上一点，且点P关于点Q的等垂点P′恰好在一次函数y=2x+3的图象上，求点P′的坐标；
（2）如图3，若点Q的坐标为（1，-2），P为直线y=2上一点，P关于点Q的等垂点P′位于y轴右侧，连接OP′，QP′，请问OP′+QP′是否有最小值？若有，请求出最小值；若无，请说明理由．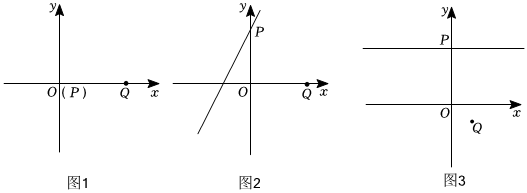
组卷：2061引用：4难度：0.3 -
28．【初步感知】
如图1，在正方形ABCD中，AD=6，点P是对角线BD上任意一点（不与B、D重合），点O是BD的中点，连接PC，过点P作PE⊥PC交直线AB于点E．
当点P与点O重合时，比较：PC PE（选填“＞”，“＜”或“=”）．
【再次感知】
如图1，当点P在线段OD上时，如何判断PC和PE数量关系呢？
甲同学通过点P分别向AB和BC作垂线，构造全等三角形，证明出PC=PE；
乙同学通过连接PA，证明出PA=PC，∠PAE=∠PEA，从而证明出PC=PE．
请选择一种思路，进行探索．
【联想感悟】
如图2，当点P落在线段OB上时，判断PC和PE的数量关系，并说明理由．
【拓展应用】
如图2，连接AP，并延长AP交直线CD于点F．
（1）若，求AE的长；DFCF=12
（2）直接写出△APE面积S的取值范围：．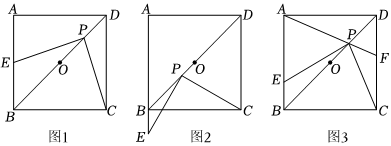
组卷：109引用：1难度：0.1
