当前位置：试卷中心 > 试卷详情

2022-2023学年山西省吕梁市孝义市八年级（下）期中数学试卷

发布：2024/9/7 8:0:8

一、选择题（每小题3分，共30分．下列各小题均给出四个备选答案，请将符合题意选项的字母代号，填写在下面方格内）

1．若二次根式
2
-
a
在实数范围内有意义，则a的取值范围是（　　）
A．a≥0 B．a＜2 C．a≥2 D．a≤2
组卷：150引用：3难度：0.5
解析
2．下列二次根式中，可以与
2
合并的是（　　）
A．
0
.
2
B．
1
2
C．
12
D．
20
组卷：724引用：6难度：0.5
解析
3．下列计算正确的是（　　）
A．
2
+
3
=
2
3
B．
5
-
3
=
2
C．
2
2
×
3
=
2
6
D．
4
2
÷
2
2
=
2
2
组卷：87引用：5难度：0.7
解析
4．下列各组数中不能作为直角三角形三边长的是（　　）
A．1.5，2，3 B．7，24，25 C．8，15，17 D．9，12，15
组卷：53引用：3难度：0.5
解析
5．如图，在△ABC中，∠ACB=90°，AC=3，BC=1，AC在数轴上，点A所表示的数为1，以点A为圆心，AB长为半径画弧，在点A左侧交数轴于点D，则点D表示的数是（　　）
A．
10
B．
-
10
C．
1
-
10
D．
10
-
1
组卷：195引用：5难度：0.6
解析
6．如图，在▱ABCD中，对角线AC、BD相交于点O，过点O作OE⊥BD交AD于点E，连接BE．若▱ABCD的周长为20，则△ABE的周长为（　　）
A．5 B．10 C．15 D．20
组卷：753引用：9难度：0.6
解析
7．在学习平行四边形时，我们先学习了平行四边形的性质定理、判定定理，再通过平行四边形边、角的特殊化，获得了特殊的平行四边形——矩形、菱形和正方形，了解了它们之间的关系，并根据它们的特殊性，得到了这些特殊的平行四边形的性质定理和判定定理．在学习这些知识的过程中，主要体现的数学思想是（　　）
A．方程思想 B．数形结合思想
C．从特殊到一般思想 D．从一般到特殊思想
组卷：34引用：3难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共7个小题，共55分．解答题应写出文字说明、证明过程或演算步骤）

21．请阅读下列材料，并完成相应任务．
勾股定理的证明
勾股定理揭示了直角三角形三条边之间的数量关系，是数学中最重要的定理之一．勾股定理的证明过程多数采用的方法是“用两种不同的方法和含有a,b,c的式子表示同一个图形的面积”，由于同一个图形的面积相等，从而得到含a,b,c的恒等式，通过化简即可完成勾股定理的证明．借助于图形的面积研究相关的数量关系，是我国古代数学研究中经常采用的重要方法，它充分显示了古人的卓越智慧．
下面是证明勾股定理的一种思路：
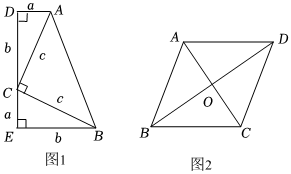
如图1，用一个等腰直角三角形（Rt△ABC），和两个全等的直角三角形（Rt△ACD，Rt△BCE）可以拼成一个直角梯形ABED．其中AD=CE=a；CD=BE=b,AC=BC=c,用两种不同的方法和含有a,b,c的式子表示梯形ABED的面积，就能完成勾股定理的证明．
提示：梯形的面积
S
=
1
2
×
（上底+下底）×高
任务：
（1）请你根据上述材料中的思路证明勾股定理；
（2）如图2，在菱形ABCD中，对角线AC、BD相交于点O，AC=12，BD=16，则AD、BC之间的距离为
．
组卷：60引用：2难度：0.5
解析
22．综合与实践
实践操作：如图1，已知矩形纸片ABCD．
第一步：如图2，将纸片沿AE折叠，使点B的对应点B′正好落在AD上，然后展平纸片，得到折痕AE；
第二步：如图3，在图2的基础上，沿DE折叠纸片，点C的对应点落在C′处，C′D与EB′交于点F．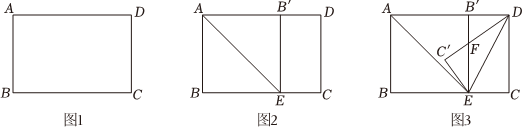

问题解决：
（1）如图2，判断四边形ABEB′的形状，并证明；
（2）如图3，证明B′F=C′F；
（3）若AB=4，BC=6，则△DEF的周长为
（直接写出答案即可）．
组卷：101引用：3难度：0.5
解析