2022-2023学年重庆市长寿区高二（下）期末数学试卷（B卷）

一、选择题（本大题共10个小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求.）

• 1．复数（1+i）（1-i）=（　　）

  A．0

  B．1

  C．2i

  D．2
  组卷：66引用：3难度：0.8

  解析

• 2．某射击运动员连续射击10次，命中环数如表：
  

  命中球数	7	8	9	10
  频数	2	3	4	1

  则这组数据的中位数和众数分别为（　　）

  A．4，4

  B．3.5，4

  C．8.5，9

  D．9，9
  组卷：34引用：2难度：0.8

  解析

• 3．下列函数是偶函数的是（　　）

  A．y=sinx

  B．y=cosx

  C．y=ex

  D．y=lnx
  组卷：194引用：3难度：0.8

  解析

• 4．某校为了了解同学们参加社会实践活动的意向，决定利用分层抽样的方法从高一、高二、高三学生中选取200人进行调查，已知该校高一年级学生有1300人，高二年级学生有1200人，高三年级学生有1500人，则抽取的学生中，高三年级有（　　）

  A．50人

  B．60人

  C．65人

  D．75人
  组卷：307引用：3难度：0.8

  解析

• 5．△ABC的内角A，B，C的对边分别为a,b,c,若

  A

  =

  30

  °

  ，

  a

  =

  2

  ，

  b

  =

  6

  ，则B=（　　）

  A．30°

  B．60°

  C．30°或150°

  D．60°或120°
  组卷：256引用：5难度：0.8

  解析

• 6．对于任意实数a,b∈R，则“a＞b”是“e^a＞e^b”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：40引用：2难度：0.8

  解析

三、解答题（本题共5小题，每小题15分，共75分.解答应写出文字说明、证明过程或演算步骤.）

• 19．若函数

  f

  （

  x

  ）

  =

  3

  sin

  （

  π

  2

  -

  2

  x

  ）

  +

  2

  sinxcosx

  ．
  （1）求函数f（x）的最小正周期；
  （2）若将函数f（x）的图象向右平移

  π

  6

  个单位后得到函数g（x）的图象，当

  x

  ∈

  [

  -

  π

  6

  ，

  π

  2

  ]

  时，求g（x）的值域．
  组卷：156引用：2难度：0.7

  解析

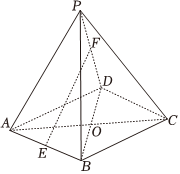• 20．如图，四棱锥P-ABCD的底面ABCD为菱形，PB=PD，E，F分别为AB和PD的中点．
  （1）求证：EF∥平面PBC；
  （2）求证：平面PBD⊥平面PAC．
  （3）若

  PA

  =

  PC

  =

  5

  ，

  AB

  =

  2

  ，

  ∠

  BAD

  =

  60

  °

  ，求二面角A-PB-C的平面角的余弦值．
  组卷：97引用：2难度：0.4

  解析