2023-2024学年广东省深圳市宝安中学九年级(上)期中数学试卷
发布:2024/10/1 11:0:2
一.选择题(每小题3分,共30分,请将正确答案填涂在答题卡上)
-
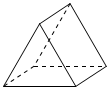 1.如图所示的几何体的俯视图是( )组卷:830引用:25难度:0.9
1.如图所示的几何体的俯视图是( )组卷:830引用:25难度:0.9 -
2.一次掷两枚质地均匀的硬币,出现两枚硬币都正面朝下的概率是( )
组卷:228引用:6难度:0.6 -
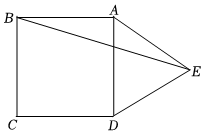 3.如图,在正方形ABCD外侧作等边△ADE,则∠AEB的度数为( )组卷:2539引用:21难度:0.8
3.如图,在正方形ABCD外侧作等边△ADE,则∠AEB的度数为( )组卷:2539引用:21难度:0.8 -
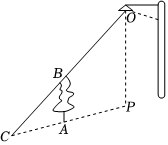 4.如图,树AB在路灯O的照射下形成投影AC,若树高AB=2m,树影AC=3m,树与路灯的水平距离AP=4.5m,则路灯的高度OP是( )组卷:826引用:5难度:0.5
4.如图,树AB在路灯O的照射下形成投影AC,若树高AB=2m,树影AC=3m,树与路灯的水平距离AP=4.5m,则路灯的高度OP是( )组卷:826引用:5难度:0.5 -
5.已知线段m、n、p、q的长度满足等式mn=pq,将它改写成比例式的形式,错误的是( )
组卷:720引用:5难度:0.9 -
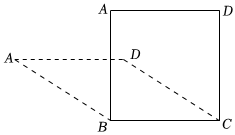 6.如图,将四根长度相等的细木条首尾顺次相接,用钉子钉成四边形ABCD,拉动木条,四边形的形状会改变.当∠A=90°时,四边形的面积为16,则当∠A=30°时,四边形的面积为( )组卷:737引用:7难度:0.5
6.如图,将四根长度相等的细木条首尾顺次相接,用钉子钉成四边形ABCD,拉动木条,四边形的形状会改变.当∠A=90°时,四边形的面积为16,则当∠A=30°时,四边形的面积为( )组卷:737引用:7难度:0.5 -
7.某校办厂生产的某种产品,今年产量为200件,计划通过改革技术,使今后两年的产量都比前一年增长一个相同的百分数,使得三年的总产量达到1400件,若设这个百分数为x,则可列方程为( )
组卷:1854引用:35难度:0.9
三.解答题(本题共7大题,55分,其中第16题8分,第17题7分;第18题6分:第19题7分:第20题8分;第21题10分;第22题9分).
-
21.梅涅劳斯(Menelaus)是古希腊数学家,他首先证明了梅涅劳斯定理,定理的内容是:如图(1),如果一条直线与△ABC的三边AB,BC,CA或它们的延长线交于F、D、E三点,那么一定有
=1.AFFB•BDDC•CEEA
下面是利用相似三角形的有关知识证明该定理的部分过程:
证明:如图(2),过点A作AG∥BC,交DF的延长线于点G,则有,AFFB=AGBD,CEEA=CDAG
∴=1.AFFB•BDDC•CEEA=AGBD•BDDC•CDAG
请用上述定理的证明方法解决以下问题:
(1)如图(3),△ABC三边CB,AB,AC的延长线分别交直线l于X,Y,Z三点,证明:=1,请用上述定理的证明方法或结论解决以下问题:BXXC•CZZA•AYYB
(2)如图(4),等边△ABC的边长为3,点D为BC的中点,点F在AB上,且BF=2AF,CF与AD交于点E,试求AE的长.
(3)如图(5),△ABC的面积为4,F为AB中点,延长BC至D,使CD=BC,连接FD交AC于E,求四边形BCEF的面积.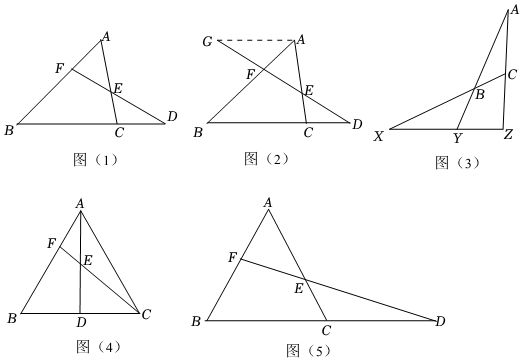 组卷:884引用:1难度:0.2
组卷:884引用:1难度:0.2 -
22.矩形ABCD中,AD=4,AB=6,点E为矩形ABCD边上的动点,连接CE.
(1)如图1,若点E在AB边上,作点B关于CE的对称点B',当点B'恰好落在对角线BD上,试求EB的长.
(2)如图2,若点E在AD边上,作点D关于CE的对称点D',连接AD'、CD'和 BD',当点E为AD的中点时,求△AD'B的面积.
(3)如图3,点E在AB边上,作点B关于CE的对称点B',射线 EB'交AD边所在直线于点G,若DG=AD,直接写出BE的值 .12 组卷:408引用:1难度:0.3
组卷:408引用:1难度:0.3


