2023年安徽省安庆市高考数学二模试卷

一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，有且只有一项符合题目要求.

• 1．已知集合M={x|

  x

  x

  -

  1

  ≤0}，

  N

  =

  {

  x

  |

  （

  2

  3

  ）

  x

  ＞

  1

  }

  ，则M∩N=（　　）

  A．∅

  B．{x|x＜0}

  C．{x|0≤x＜1}

  D．{x|0＜x＜1}
  组卷：91引用：2难度：0.8

  解析

• 2．若复数z满足

  i

  ⋅

  z

  =

  2022

  +

  i

  2023

  （i是虚数单位），z的共轭复数是

  z

  ，则

  z

  -

  z

  的模是（　　）

  A． 4044 2 + 4

  B．4044

  C．2

  D．0
  组卷：83引用：3难度：0.9

  解析

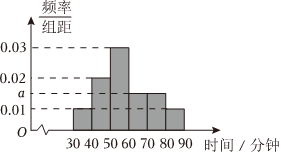• 3．为了解学生每天的体育活动时间，某市教育部门对全市高中学生进行调查，随机抽取1000名学生每天进行体育运动的时间，按照时长（单位：分钟）分成6组：第一组[30，40），第二组[40，50），第三组[50，60），第四组[60，70），第五组[70，80），第六组[80，90]．对统计数据整理得到如图所示的频率分布直方图，则可以估计该市高中学生每天体育活动时间的第25百分位数约为（　　）

  A．43.5分钟

  B．45.5分钟

  C．47.5分钟

  D．49.5分钟
  组卷：114引用：3难度：0.7

  解析

• 4．已知非零向量

  a

  ，

  b

  的夹角为θ，

  |

  a

  +

  b

  |

  =

  2

  ，且|

  a

  ||

  b

  |≥

  4

  3

  ．则夹角θ的最小值为（　　）

  A． π 6

  B． π 4

  C． π 3

  D． π 2
  组卷：70引用：2难度：0.5

  解析

• 5．已知第二象限角α满足

  sin

  （

  π

  +

  α

  ）

  =

  -

  2

  3

  ，则sin2β-2sin（α+β）cos（α-β）的值为（　　）

  A． - 1 9

  B． - 4 5 9

  C． 1 9

  D． 4 5 9
  组卷：140引用：2难度：0.6

  解析

• 6．已知等差数列{a_n}满足

  a

  2

  1

  +

  a

  2

  4

  =4，则a₂+a₃不可能取的值是（　　）

  A．-3

  B．-2 2

  C． 3 2

  D． 2
  组卷：98引用：3难度：0.7

  解析

• 7．已知函数f（x）=

  x | lnx | ， x ＞ 0

  - x e x ， x ＜ 0

  ，若函数g（x）=f（x）-|x²-kx|恰有3个零点，则实数k的取值范围是（　　）

  A．（-∞，-1）∪（1，+∞）	B．（1，+∞）
  C．（-∞，-1]∪（1，+∞）	D．（-∞，-1）∪[1，+∞）
  组卷：264引用：5难度：0.5

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

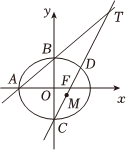• 21．如图，在平面直角坐标系xOy中，A、B、C分别为椭圆E：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的三个顶点，F（c,0）为其右焦点，直线AB与直线CF相交于点T．
  （1）若点T在直线l：x=

  a

  2

  c

  上，求椭圆E的离心率；
  （2）设直线CF与椭圆E的另一个交点为D，M是线段CD的中点，椭圆E的离心率为

  1

  2

  ，试探究

  |

  TM

  |

  |

  CD

  |

  的值是否为定值（与a,b无关）．若为定值，求出该定值；若不为定值，请说明理由．
  组卷：82引用：2难度：0.2

  解析

• 22．已知函数f（x）=alnx+bx²e^1-x，a,b∈R．e≈2.71828⋯．
  （1）若曲线y=f（x）在点（2，f（2））处的切线方程是y=x+ln2，求a和b的值；
  （2）若a=e,且f（x）的导函数f'（x）恰有两个零点，求b的取值范围．
  组卷：60引用：2难度：0.4

  解析