2022-2023学年四川省眉山市仁寿一中南校区高一(下)期末数学试卷
发布:2024/6/1 8:0:9
一、单项选择题(本大题共8小题,每小题5分,共40分.在每个小题给出的四个选项中,只有一项符合题目要求.)
-
1.已知复数z满足z=
,那么z的共轭复数在复平面上对应的点位于( )2i1+i组卷:143引用:11难度:0.9 -
2.已知一组数据x1,x2,⋯,xn的平均数为
,标准差为s,则数据2x1+1,2x2+1,⋯,2xn+1的平均数和方差分别为( )x组卷:105引用:5难度:0.8 -
3.已知m,n是不重合的直线,α,β是不重合的平面,则下列结论中正确的是( )
组卷:140引用:6难度:0.8 -
4.已知
,则tanα=-32=( )sinα+2cosαcosα-sinα组卷:363引用:3难度:0.7 -
5.在正四棱台ABCD-A1B1C1D1中,AB=4,A1B1=AA1=2,则该四棱台的体积为( )
组卷:214引用:5难度:0.7 -
6.为测量河对岸的直塔AB的高度,选取与塔底B在同一水平面内的两个测量基点C,D,测得∠BCD的大小为60°,点C,D的距离为200m,在点C处测得塔顶A的仰角为45°,在点D处测得塔顶A的仰角为30°,则直塔AB的高为( )
组卷:144引用:4难度:0.7 -
7.在△ABC在中,点D线段BC上任意一点,点D满足
,若存在实数m和n,使得AD=3AP,则m+n=( )BP=mAB+nAC组卷:200引用:6难度:0.7
四、解答题(本大题共6小题,第17题10分,18-22题每题12分,共70分.把必要的解答过程写在答题卡相应位置上)
-
21.已知平面向量
,m=(2-sin(2x+π6),-2),n=(1,sin2x).f(x)=m•n
(1)求函数f(x)的单调增区间,其中;x∈[0,π2]
(2)将函数f(x)的图象所有的点向右平移个单位,再将所得图象上各点横坐标缩短为原来的π12(纵坐标不变),再向下平移1个单位得到g(x)的图象,若g(x)=m在12上恰有2个解,求m的取值范围.x∈[-π8,5π24]组卷:140引用:4难度:0.6 -
22.在《九章算术•商功》中,将四个面都是直角三角形的三棱锥称为“鳖臑”.如图,现将一矩形ABCD沿着对角线BD将△ABD折成△PBD,且点P在平面BCD内的投影H在线段DC上.已知AB=2,AD=1.
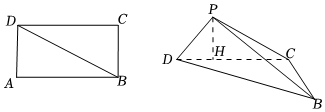
(1)证明:三棱锥P-BCD为鳖臑;
(2)求二面角P-BD-C的正弦值.组卷:30引用:1难度:0.5


