当前位置：试卷中心 > 试卷详情

2022-2023学年辽宁省丹东市五校高三（上）联考数学试卷

发布：2024/7/25 8:0:9

1．已知集合
A
=
{
x
∈
Z
|
-
2
≤
x
＜
3
}
，
B
=
{
x
|
y
=
1
-
lnx
}
，则A∩B=（　　）
A．{-2，-1，0，1，2} B．{1，2}
C．[-2，e] D．（0，e]
组卷：4引用：3难度：0.8
解析
2．已知角α的顶点与坐标原点O重合，始边与x轴的非负半轴重合．若角α终边上一点P的坐标为
（
cos
2
π
3
，
sin
2
π
3
）
，则sinαtanα=（　　）
A．
-
3
2
B．
-
3
2
C．
3
2
D．
3
2
组卷：42引用：6难度：0.7
解析
3．下列结论中，错用基本不等式做依据的是（　　）
A．a,b均为负数，则
2
a
b
+
b
2
a
≥
2
B．
x
2
+
2
x
2
+
1
≥
2
C．
sinx
+
4
sinx
≥
4
D．
a
∈
R
+
，
（
3
-
a
）
（
1
-
3
a
）
≤
0
组卷：79引用：6难度：0.7
解析
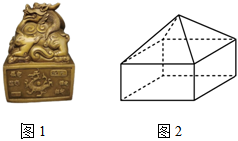4．我国有着丰富悠久的“印章文化”，古时候的印章一般用贵重的金属或玉石制成，本是官员或私人签署文件时代表身份的信物，后因其独特的文化内涵，也被作为装饰物来使用．图1是明清时期的一个金属印章摆件，除去顶部的环以后可以看作是一个正四棱柱和一个正四棱锥组成的几何体，如图2．已知正四棱柱和正四棱锥的高相等，且底面边长均为4，若该几何体的所有顶点都在同一个球面上，则这个球的表面积是（　　）
A．12π B．24π C．36π D．48π
组卷：771引用：5难度：0.6
解析

5．下列结论正确的是（　　）

A．若A，B，C是一组两两相互独立的事件，则P（ABC）=P（A）P（B）P（C）

B．若A，B事件满足P（A）+P（B）=1，则A，B是对立事件

C．若A，B是互斥事件，则

（

∪

）

D．“A，B是互斥事件”是“A，B是对立事件”的充分不必要条件

组卷：132引用：3难度：0.7

6．已知非零向量
a
，
b
的夹角正切值为
2
6
，且
（
a
+
3
b
）
⊥
（
2
a
-
b
）
，则
|
a
|
|
b
|
=（　　）
A．2 B．
2
3
C．
3
2
D．1
组卷：88引用：11难度：0.6
解析
7．已知等比数列{a_n}中，a_n＞0，其前n项和为S_n，前n项积为T_n，且S₂=48，S₄=60，则使得T_n＜1成立的正整数n的最小值为（　　）
A．9 B．10 C．11 D．12
组卷：289引用：6难度：0.6
解析

21．2021年5月12日，2022北京冬奥会和冬残奥会吉祥物“冰墩墩”、“雪容融”亮相上海展览中心．为了庆祝吉祥物在上海的亮相，某商场举办了赢取冰墩墩、雪容融吉祥物挂件答题活动．为了提高活动的参与度，计划有
1
3
的人只能赢取冰墩墩挂件，另外
2
3
的人计划既能赢取冰墩墩挂件又能赢取雪容融挂件，每位顾客只能赢取冰墩墩挂件，则记1分，若既能赢取冰墩墩挂件又能赢取雪容融挂件，则记2分，假设每位顾客能赢取冰墩墩挂件和赢取雪容融挂件相互独立，视频率为概率．
（1）从顾客中随机抽取3人，记这3人的合计得分为X，求X的分布列和数学期望；
（2）从顾客中随机抽取n人（n∈N^*），记这n人的合计得分恰为n+1分的概率为P_n，求P₁+P₂+…+P_n．
组卷：128引用：4难度：0.5
解析
22．已知函数f（x）=ae^x-（1-a）x.
（1）讨论f（x）的单调性；
（2）当a=1时，若函数y=f（x）-e^t（lnx+t）有两个零点，求实数t的取值范围．
组卷：63引用：4难度：0.5
解析

A．{-2，-1，0，1，2}	B．{1，2}
C．[-2，e]	D．（0，e]