当前位置：试卷中心 > 试卷详情

2022-2023学年湖南省长沙市师大思沁高级中学高一（下）期末数学试卷

发布：2024/6/8 8:0:9

1．已知i是虚数单位，复数
z
=
i
i
+
1
，则z的虚部为（　　）
A．
1
2
i
B．
-
1
2
i
C．
1
2
D．
-
1
2
组卷：53引用：8难度：0.9
解析
2．在锐角三角形ABC中，a=2bsinA，则B=（　　）
A．
π
6
B．
π
4
C．
π
3
D．
7
π
12
组卷：334引用：7难度：0.7
解析
3．甲、乙两人独立地破译某个密码，甲译出密码的概率为0.4，乙译出密码的概率为0.5．则密码被破译的概率为（　　）
A．0.9 B．0.8 C．0.7 D．0.2
组卷：78引用：3难度：0.8
解析
4．若m、n、l表示不同的直线，α、β表示不同的平面，则下列推理正确的是（　　）
A．若m∥α，n∥α，则m∥n B．若m⊥α，n⊥α，则m∥n
C．若m⊥l,n⊥l,则m∥n D．若m∥α，m∥β，则α∥β
组卷：53引用：2难度：0.5
解析
5．在△ABC中，
BD
=
2
DA
，若
CB
=
λ
CA
+
μ
CD
，则
λ
μ
的值为（　　）
A．
-
2
3
B．
-
3
2
C．
2
3
D．
3
2
组卷：226引用：4难度：0.7
解析
6．已知某19个数据的平均数为5，方差为2，现加入一个数5，此时这20个数据的平均数为
x
，方差为s²，则（　　）
A．
x
=5，s²=2 B．
x
=5，s²＞2 C．
x
=5，s²＜2 D．
x
＞5，s²＜2
组卷：217引用：6难度：0.8
解析
7．在一个正三棱柱中，所有棱长都为2，各顶点都在同一个球面上，则该球的表面积为（　　）
A．
21
π
3
B．
28
π
3
C．
56
π
3
D．
7
21
π
3
组卷：209引用：4难度：0.5
解析

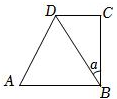21．在四边形ABCD中，AB=2，∠A=60°，∠ABC=∠BCD=90°，设∠CBD=α．
（1）当α=15°时，求线段AD的长度；
（2）求△BCD面积的最大值．
组卷：87引用：3难度：0.5
解析
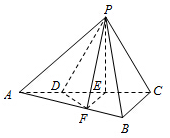22．如图，三棱锥P-ABC中，平面PAC⊥平面ABC，∠ABC=
π
2
，点D、E在线段AC上，且AD=DE=EC=2，PD=PC=4，点F在线段AB上，且EF∥BC．
（Ⅰ）证明：AB⊥平面PFE．
（Ⅱ）若四棱锥P-DFBC的体积为7，求线段BC的长．
组卷：6652引用：30难度：0.5
解析

A．若m∥α，n∥α，则m∥n	B．若m⊥α，n⊥α，则m∥n
C．若m⊥l,n⊥l,则m∥n	D．若m∥α，m∥β，则α∥β

1．已知i是虚数单位，复数z=ii+1，则z的虚部为（ ）