当前位置：试卷中心 > 试卷详情

2022-2023学年北京市海淀区科技大学附中七年级（下）期末数学试卷

发布：2024/7/14 8:0:9

一、选择题（共10小题；共50分）

1．（a²）⁴等于（　　）
A．2a⁴ B．4a² C．a⁸ D．a⁶
组卷：94引用：12难度：0.9
解析
2．下列调查中，须用普查的是（　　）
A．了解某市学生的视力情况
B．了解某市中学生课外阅读的情况
C．了解某市百岁以上老人的健康情况
D．了解某市老年人参加晨练的情况
组卷：873引用：97难度：0.9
解析
3．不等式组
x
-
1
＞
3
2
-
2
x
＜
4
的解集是（　　）
A．x＞4 B．x＞-1 C．-1＜x＜4 D．x＜-1
组卷：704引用：12难度：0.6
解析
4．计算-3（a+b）•[-2（a+b）²]，结果等于（　　）
A．-6（a+b）³ B．-6（a³+b³） C．6（a+b）³ D．6（a³+b³）
组卷：223引用：1难度：0.9
解析
5．下列各组数是二元一次方程组
x
+
3
y
=
7
y
-
x
=
1
的解的是（　　）
A．
x
=
1
y
=
2
B．
x
=
0
y
=
1
C．
x
=
7
y
=
0
D．
x
=
1
y
=
-
2
组卷：821引用：21难度：0.9
解析
6．如图，直线a、b被直线c所截，下列说法正确的是（　　）
A．当∠1=∠2时，一定有a∥b
B．当a∥b时，一定有∠1=∠2
C．当a∥b时，一定有∠1+∠2=90°
D．当∠1+∠2=180°时，一定有a∥b
组卷：736引用：30难度：0.9
解析
7．小石将（2020x+2021）²展开后得到多项式a₁x²+b₁x+c₁，小明将（2021x-2020）²展开后得到多项式a₂x²+b₂x+c₂，若两人计算过程无误，则a₁-a₂的值为（　　）
A．-1 B．-4041 C．4041 D．1
组卷：478引用：2难度：0.6
解析
8．如图，图中∠1与∠2是同位角的序号是（　　）
A．②③ B．②③④ C．①②④ D．③④
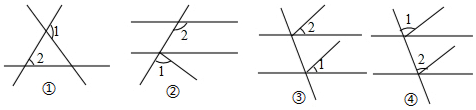组卷：1055引用：6难度：0.7
解析
9．某餐饮公司为一所学校提供午餐，有10元、12元、15元三种价格的盒饭供师生选择，每人选一份，该校师生某一天购买的这三种价格盒饭数依次占50%、30%、20%，那么这一天该校师生购买盒饭费用的平均数和中位数分别是（　　）
A．12元、12元 B．12元、11元
C．11.6元、12元 D．11.6元、11元
组卷：573引用：5难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共12小题；共156分）

27．如图，已知AB∥CD，猜想图①，图②，图③中，∠B，∠E，∠D之间有何数量关系？请用等式表示出它们的关系，并选择其中的两个等式说明理由．
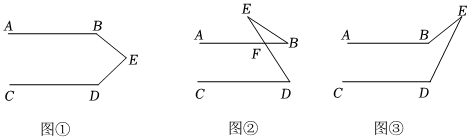组卷：309引用：2难度：0.7
解析
28．如果一个正整数能表示为两个连续奇数的平方差，那么称这个正整数为“奇特数”．例如：
8=3²-1²，16=5²-3²，24=7²-5²；则8、16、24这三个数都是奇特数．
（1）32和2012这两个数是奇特数吗？若是，表示成两个连续奇数的平方差形式．
（2）设两个连续奇数是2n-1和2n+1（其中n取正整数），由这两个连续奇数构造的奇特数是8的倍数吗？为什么？
组卷：1241引用：3难度：0.5
解析