当前位置：试卷中心 > 试卷详情

2023-2024学年湖南省长沙市开福区青竹湖湘一外国语学校九年级（上）入学数学试卷

发布：2024/7/26 8:0:9

一、选择题

1．3的绝对值是（　　）
A．-3 B．3 C．
1
3
D．
-
1
3
组卷：165引用：15难度：0.9
解析
2．若代数式
x
-
1
在实数范围内有意义，则x的取值范围是（　　）
A．x＜1 B．x≤1 C．x＞1 D．x≥1
组卷：1146引用：65难度：0.9
解析
3．下列计算正确的是（　　）
A．x²•x³=x⁶ B．（x+2y）²=x²+2xy+4y²
C．（mn-3）（mn+3）=mn²-9 D．（-3xy²）²÷（x²y）=9y³
组卷：158引用：3难度：0.7
解析
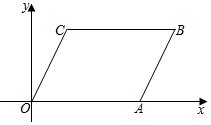4．如图，四边形ABCO为平行四边形，A，C两点的坐标分别是（3，0），（1，2），则平行四边形ABCO的周长等于（　　）
A．
5
B．
3
C．4
5
D．6+2
5
组卷：1018引用：6难度：0.7
解析
5．下列函数图象中，当x＞0时，y随x的增大而减小的是（　　）
A．y=2x+1 B．y=x C．y=x² D．y=-（x+1）²
组卷：393引用：1难度：0.6
解析
6．一组数据4，5，6，7，7，8的中位数和众数分别是（　　）
A．7，7 B．7，6.5 C．5.5，7 D．6.5，7
组卷：174引用：61难度：0.9
解析
7．已知α，β是一元二次方程x²+x-2=0的两个实数根，则α+β-αβ的值是（　　）
A．3 B．1 C．-1 D．-3
组卷：3850引用：20难度：0.9
解析
8．某厂一月份生产某大型机器2台，计划二、三月份共生产9台，设二、三月份每月生产台数的月平均增长率为x,根据题意列出的方程是（　　）
A．2（1+x）²=9 B．2（1-x）²=9
C．2（1+x）+2（1+x）²=9 D．2+2（1+x）+2（1+x）²=9
组卷：72引用：2难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题

24．在平面直角坐标系中，如果点P的横坐标和纵坐标相等，则称点P为平衡点．例如：点（1，1），（
-
2
，
-
2
），……都是平衡点．
（1）判断函数y=2x+1的图象上是否存在平衡点，若存在，求出其平衡点的坐标；
（2）若二次函数y=ax²+6x+c（a≠0）的图象上有且只有一个平衡点
（
5
2
，
5
2
）
．
①求a,c的值；
②若1≤x≤m时，函数
y
=
a
x
2
+
6
x
+
c
+
1
4
（a≠0）的最小值为-1，最大值为3，求实数m的取值范围．
组卷：424引用：1难度：0.2
解析
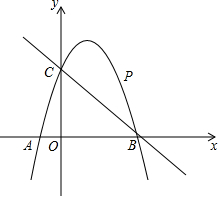25．如图，已知二次函数y=ax²+2x+c的图象经过点C（0，3），与x轴分别交于点A，点B（3，0）．点P是直线BC上方的抛物线上一动点．
（1）求二次函数y=ax²+2x+c的表达式；
（2）连接PO，PC，并把△POC沿y轴翻折，得到四边形POP′C．若四边形POP′C为菱形，请求出此时点P的坐标；
（3）当点P运动到什么位置时，四边形ACPB的面积最大？求出此时P点的坐标和四边形ACPB的最大面积．
组卷：3476引用：22难度：0.1
解析