当前位置：试卷中心 > 试卷详情

2022-2023学年四川省达州市达川区百节中心学校八年级（下）期末数学试卷

发布：2024/7/18 8:0:9

1．下列电视台的台标，是中心对称图形的是（　　）
A． B． C． D．
组卷：158引用：22难度：0.8
解析
2．不等式x＞1的解集在数轴上表示正确的是（　　）
A． B． C． D．
组卷：72引用：4难度：0.9
解析
3．下列各式中，能用完全平方公式分解因式的是（　　）
A．4x²-4x+1 B．6x²+3x+1 C．x²+4xy+2y² D．9x²+18x+1
组卷：342引用：3难度：0.8
解析
4．如图，在△ABC中，AB=AC，∠A=120°，BC=6cm,AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN的长为（　　）
A．4cm B．3cm C．2cm D．1cm
组卷：7114引用：142难度：0.9
解析
5．一个多边形的每个外角都等于60°，则这个多边形的边数为（　　）
A．8 B．7 C．6 D．5
组卷：995引用：75难度：0.7
解析
6．下列变形中，正确的是（　　）
A．-
1
a
=
-
1
a
B．
1
a
+
1
b
=
1
a
+
b
C．
2
b
2
a
2
=
2
b
a
D．
a
+
ab
b
+
ab
=
a
b
组卷：157引用：4难度：0.9
解析
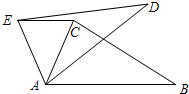7．如图在△ABC中，∠CAB=70°，在同一平面内，将△ABC绕点A逆时针旋转到△ADE的位置，使得EC∥AB，则∠CAE度数为（　　）
A．30° B．35° C．40° D．50°
组卷：250引用：5难度：0.7
解析
8．关于x的分式方程
2
x
-
a
x
+
1
=1的解为正数，则字母a的取值范围为（　　）
A．a≥-1 B．a＞-1 C．a≤-1 D．a＜-1
组卷：10215引用：64难度：0.9
解析

24．某校为美化校园，计划对面积为1800m²的区域进行绿化，安排甲、乙两个工程队完成．已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且在独立完成面积为400m²区域的绿化时，甲队比乙队少用4天．
（1）求甲、乙两工程队每天能完成绿化的面积分别是多少m²？
（2）若学校每天需付给甲队的绿化费用为0.4万元，乙队为0.25万元，要使这次的绿化总费用不超过8万元，至少应安排甲队工作多少天？
组卷：12250引用：126难度：0.3
解析
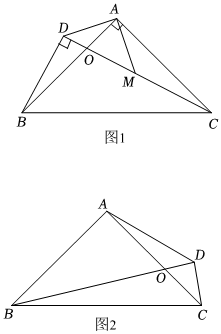25．如图，在Rt△ABC中，∠BAC=90°，AB=AC，在BC的同侧作任意Rt△DBC，∠BDC=90°．
（1）若CD=2BD，M是CD中点（如图1），求证：AD=AM；
下面是小明的证明过程，请你将它补充完整：
证明：设AB与CD相交于点O，
∵∠BDC=90°，∠BAC=90°，
∴∠DOB+∠DBO=∠AOC+∠ACO=90°．
∵∠DOB=∠AOC，
∴∠DBO=∠
．
∵M是DC的中点，CD=2BD，
∴CM=
1
2
CD=
．
又∵AB=AC，
∴△ADB≌△AMC．
∴AD=AM．
（2）若CD＜BD（如图2），在BD上是否存在一点N，使得△ADN是以DN为斜边的等腰直角三角形？若存在，请在图2中确定点N的位置，并加以证明；若不存在，请说明理由；
（3）当CD≠BD时，线段AD，BD与CD满足怎样的数量关系？请直接写出．
组卷：40引用：1难度：0.3
解析