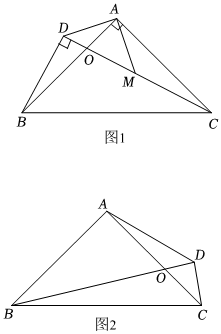
如图，在Rt△ABC中，∠BAC=90°，AB=AC，在BC的同侧作任意Rt△DBC，∠BDC=90°．
（1）若CD=2BD，M是CD中点（如图1），求证：AD=AM；
下面是小明的证明过程，请你将它补充完整：
证明：设AB与CD相交于点O，
∵∠BDC=90°，∠BAC=90°，
∴∠DOB+∠DBO=∠AOC+∠ACO=90°．
∵∠DOB=∠AOC，
∴∠DBO=∠MCAMCA．
∵M是DC的中点，CD=2BD，
∴CM=12CD=BDBD．
又∵AB=AC，
∴△ADB≌△AMC．
∴AD=AM．
（2）若CD＜BD（如图2），在BD上是否存在一点N，使得△ADN是以DN为斜边的等腰直角三角形？若存在，请在图2中确定点N的位置，并加以证明；若不存在，请说明理由；
（3）当CD≠BD时，线段AD，BD与CD满足怎样的数量关系？请直接写出．
1
2
【考点】三角形综合题．
【答案】MCA；BD
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/17 8:0:9组卷：40引用：1难度：0.3
相似题
-
1．在△ABC中，∠BAC=90°，AB=AC，点D在△ABC外部且AD⊥CD．
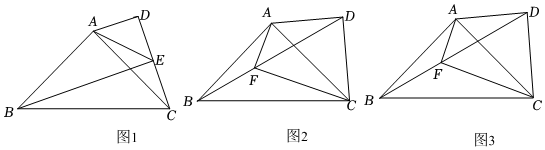
（1）如图1，若BE∥AD交CD于点E，求证：AD=DE；
（2）如图2，连接BD，点F在BD上且∠AFC=90°，若AF=3，求△ABF的面积；
（3）在（2）的条件下，若3BF=2DF，求AD的长．发布：2025/6/19 21:30:2组卷：199引用：1难度：0.2 -
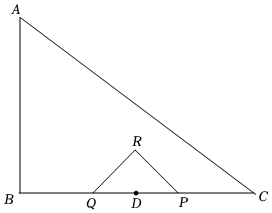2．在Rt△ABC中，∠B=90°，AB=3，BC=4，点D为BC边中点，点P从点D出发沿D-C-B的方向以每秒2个单位的速度向终点B运动，点Q从点D出发沿射线DB的方向以每秒2个单位的速度运动，当点P到达点B时，P、Q同时停住运动，以PQ为斜边在PQ的上方作等腰直角三角形PQR，设运动时间为t秒（t＞0）．
（1）用含t的代数式表示PC的长；
（2）当点R落在AC上时，求t的值；
（3）设△ABC的重心为点O，当点O落在△PQR内部时，求t的取值范围；
（4）设PR的中点为点M，当直线CM将△PQR的面积分成1：5的两部分时，直接写出t的值．发布：2025/6/19 21:30:2组卷：13引用：1难度：0.1 -
3．△ABC是等边三角形，点D、E分别在边AB、BC上，若BD=EC．
（1）如图1，求证：∠AFD=60°；
（2）如图2，FH为∠AFC的平分线，点H在FM的延长线上，连接HA、HC，∠AHC+∠AFC=180°，求证：AF+CF=FH；
（3）如图3，在（2）的条件下，延长AF交CH的延长线于点K，点G在线段AH上，GH=CK，连接CG交FH于点M，FN=3，AK=8，求FH的长．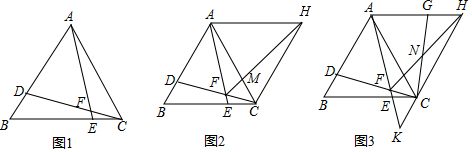
发布：2025/6/19 22:30:1组卷：480引用：2难度：0.1
