2022-2023学年辽宁省沈阳市和平区宇光中学九年级（上）第三次月考数学试卷

一、选择题（共30分）

• 1．估计

  7

  +1的值（　　）

  A．在1和2之间

  B．在2和3之间

  C．在3和4之间

  D．在4和5之间
  组卷：3026引用：60难度：0.7

  解析

• 2．中国华为麒麟985处理器是采用7纳米制程工艺的手机芯片，在指甲盖大小的尺寸上塞进了120亿个晶体管，是世界上最先进的具有人工智能的手机处理器，将120亿个用科学记数法表示为（　　）

  A．1.2×109个

  B．12×109个

  C．1.2×1010个

  D．1.2×1011个
  组卷：674引用：42难度：0.8

  解析

• 3．如图是由10个同样大小的小正方体摆成的几何体．将小正方体①移走后，则关于新几何体的三视图描述正确的是（　　）

  A．俯视图不变，左视图不变

  B．主视图改变，左视图改变

  C．俯视图不变，主视图不变

  D．主视图改变，俯视图改变
  组卷：437引用：9难度：0.8

  解析

• 4．如果a＞b,c＜0，那么下列不等式成立的是（　　）

  A．a+c＞b	B．a+c＞b-c
  C．ac-1＞bc-1	D．a（c-1）＜b（c-1）
  组卷：1839引用：18难度：0.8

  解析

• 5．李老师为了了解本班学生每周课外阅读文章的数量，抽取了7名同学进行调查，调查结果如下（单位：篇/周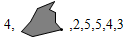）：，其中有一个数据不小心被墨迹污损．已知这组数据的平均数为4，那么这组数据的众数与中位数分别为（　　）

  A．5，4

  B．3，5

  C．4，4

  D．4，5
  组卷：818引用：6难度：0.7

  解析

• 6．如图，四边形AOEF是平行四边形，点B为OE的中点，延长FO至点C，使FO=3OC，连接AB、AC、BC，则在△ABC中，S_△ABO：S_△AOC：S_△BOC=（　　）

  A．6：2：1

  B．3：2：1

  C．6：3：2

  D．4：3：2
  组卷：5002引用：17难度：0.5

  解析

• 7．若数a使关于x的不等式组

  x 3 - 2 ≤ 1 4 （ x - 7 ） ，

  6 x - 2 a ＞ 5 （ 1 - x ）

  有且仅有三个整数解，且使关于y的分式方程

  1

  -

  2

  y

  y

  -

  1

  -

  a

  1

  -

  y

  =-3的解为正数，则所有满足条件的整数a的值之和是（　　）

  A．-3

  B．-2

  C．-1

  D．1
  组卷：3630引用：7难度：0.5

  解析

• 8．如图，在Rt△ABC中，∠C=90°，AB=5，BC=4．点P是边AC上一动点，过点P作PQ∥AB交BC于点Q，D为线段PQ的中点，当BD平分∠ABC时，AP的长度为（　　）

  A． 8 13

  B． 15 13

  C． 25 13

  D． 32 13
  组卷：6156引用：32难度：0.6

  解析

三、解答题（共66分）

• 25．在一堂数学实践课上，赵老师给出了下列问题：
  【提出问题】
  （1）如图1，在△ABC中，E是BC的中点，P是AE的中点，就称CP是△ABC的“双中线”，∠ACB=90°，AC=3，AB=5．则CP=

  ．
  【探究规律】
  （2）在图2中，E是正方形ABCD一边上的中点，P是BE上的中点，则称AP是正方形ABCD的“双中线”，若AB=4．则AP的长为

  （按图示辅助线求解）；
  （3）在图3中，AP是矩形ABCD的“双中线”，若AB=4，BC=6，请仿照（2）中的方法求出AP的长，并说明理由；
  【拓展应用】
  （4）在图4中，AP是平行四边形ABCD的“双中线”，若AB=4，BC=10，∠BAD=120°．求出△ABP的周长，并说明理由？
  
  组卷：494引用：9难度：0.1

  解析

• 26．如果抛物线C₁的顶点在抛物线C₂上，抛物线C₂的顶点也在抛物线C₁上时，那么我们称抛物线C₁与C₂“互为关联”的抛物线．如图1，已知抛物线C₁：y₁=

  1

  4

  x²+x与C₂：y₂=ax²+x+c是“互为关联”的抛物线，点A，B分别是抛物线C₁，C₂的顶点，抛物线C₂经过点D（6，-1）．
  （1）直接写出A，B的坐标和抛物线C₂的解析式；
  （2）抛物线C₂上是否存在点E，使得△ABE是直角三角形？如果存在，请求出点E的坐标；如果不存在，请说明理由；
  （3）如图2，点F（-6，3）在抛物线C₁上，点M，N分别是抛物线C₁，C₂上的动点，且点M，N的横坐标相同，记△AFM面积为S₁（当点M与点A，F重合时S₁=0），△ABN的面积为S₂（当点N与点A，B重合时，S₂=0），令S=S₁+S₂，观察图象，当y₁≤y₂时，写出x的取值范围，并求出在此范围内S的最大值．
  
  组卷：2434引用：6难度：0.1

  解析