2022-2023学年安徽省安庆七中高二（下）月考数学试卷（3月份）

一、单选题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一个是符合题目要求的.）

• 1．已知集合A={x|x²-9x-10≤0}，B={x|x＞1}，则A∪B=（　　）

  A．（1，10]

  B．（1，+∞）

  C．[-1，10]

  D．[-1，+∞）
  组卷：54引用：3难度：0.9

  解析

• 2．复数z在复平面内对应的点为（-1，2），则

  1

  -

  i

  z

  +

  i

  =（　　）

  A． 1 5 - 1 5 i

  B． 1 5 - 2 5 i

  C． - 2 5 - 1 5 i

  D． - 1 5 - 1 5 i
  组卷：33引用：4难度：0.8

  解析

• 3．下列说法中正确的是（　　）

  A．若事件A与事件B是互斥事件，则P（A）+P（B）=1

  B．对于事件A和B，P（A∪B）=P（A）+P（B）

  C．一个人打靶时连续射击两次，则事件“至少有一次中靶”与事件“至多有一次中靶”是对立事件

  D．把红、橙、黄、绿4张纸牌随机分给甲、乙、丙、丁4人，每人分得1张，则事件“甲分得红牌”与事件“乙分得红牌”是互斥事件
  组卷：52引用：3难度：0.8

  解析

• 4．设x,y∈R，向量

  a

  =

  （

  x

  ,

  2

  ）

  ，

  b

  =

  （

  1

  ，

  y

  ）

  ，

  c

  =

  （

  -

  2

  ，

  2

  ）

  ，且

  a

  ⊥

  c

  ，

  b

  ∥

  c

  ，则x+y=（　　）

  A．0

  B．1

  C．2

  D．3
  组卷：61引用：2难度：0.7

  解析

• 5．给出下列四个说法，其中正确说法的序号为（　　）
  ①平行于同一直线的两平面平行；
  ②平行于同一平面的两平面平行；
  ③垂直于同一直线的两平面平行；
  ④垂直于同一平面的两平面平行

  A．①②

  B．②③

  C．①②③

  D．②③④
  组卷：3引用：2难度：0.7

  解析

• 6．已知{a_n}为等比数列，a₅+a₈=-3，a₆a₇=-18，则a₂+a₁₁=（　　）

  A．3

  B．-9

  C． 21 2

  D．- 21 2
  组卷：369引用：2难度：0.7

  解析

• 7．若f′（x）是函数f（x）的导数，且f′（a）=-1，则

  x

  →

  a

  lim

  f

  （

  3

  x

  -

  2

  a

  ）

  -

  f

  （

  3

  a

  -

  2

  x

  ）

  x

  -

  a

  =（　　）

  A．-5

  B．-4

  C．-1

  D．0
  组卷：178引用：2难度：0.9

  解析

四、解答题（本大题共6小题，第17题10分，其余5小题均12分，共70分.）

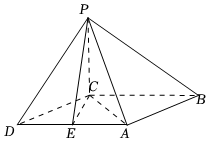• 21．如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，AD=2，

  AB

  =

  2

  ，

  ∠

  ABC

  =

  π

  4

  ，平面PAC⊥平面ABCD．
  （1）证明：AB⊥PC；
  （2）若PA=PD=2，E为AD的中点，求三棱锥A-PCE的体积．
  组卷：41引用：2难度：0.6

  解析

• 22．已知数列{a_n}满足对任意的n∈N*，都有

  a

  3

  1

  +

  a

  3

  2

  +…+

  a

  3

  n

  =（a₁+a₂+…+a_n）²，且a_n＞0．
  （1）求数列{a_n}的通项公式；
  （2）设数列

  {

  1

  a

  n

  a

  n

  +

  2

  }

  的前n项和为S_n，不等式S_n＞

  1

  3

  lo

  g

  a

  （

  1

  -

  a

  ）

  对任意的正整数n恒成立，求实数a.
  组卷：26引用：1难度：0.5

  解析