2022-2023学年广东省东莞市东华初级中学思维班八年级（下）月考数学试卷（4月份）

一、选择题（每小题3分，共30分）

• 1．如图图形既是轴对称图形又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：14引用：1难度：0.9

  解析

• 2．用配方法解一元二次方程x²-4x-1=0，配方后得到的方程是（　　）

  A．（x-2）2=1

  B．（x-2）2=4

  C．（x-2）2=3

  D．（x-2）2=5
  组卷：651引用：90难度：0.9

  解析

• 3．如果4是关于x的一元二次方程x²-6x+k=0的一个根，则方程的另一个根是（　　）

  A．2

  B．3

  C．4

  D．5
  组卷：156引用：2难度：0.7

  解析

• 4．下列抛物线中，其顶点是抛物线的最高点的是（　　）

  A．y=x2

  B． y = 1 2 x 2 + 1

  C．y=-5+x2

  D．y=-x2-1
  组卷：139引用：5难度：0.6

  解析

• 5．将抛物线y=-5x²+1先向左平移3个单位，再向下平移2个单位，所得抛物线的解析式为（　　）

  A．y=-5（x+3）2-2	B．y=-5（x+3）2-1
  C．y=-5（x-3）2-2	D．y=-5（x-3）2-1
  组卷：389引用：9难度：0.7

  解析

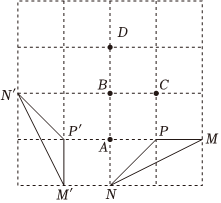• 6．如图，在4×4的正方形网格中，△MPN绕某点旋转一定的角度，得到△M'P'N'，其旋转中心是（　　）

  A．点A

  B．点B

  C．点C

  D．点D
  组卷：806引用：8难度：0.5

  解析

• 7．关于一元二次方程x²+4x+3=0根的情况，下列说法中正确的是（　　）

  A．有两个不相等的实数根	B．有两个相等的实数根
  C．没有实数根	D．无法确定
  组卷：1061引用：17难度：0.6

  解析

五、解答题（每小题12分，共24分）

• 22．综合与实践
  问题情境：如图1，四边形ABCD和EFCG都是正方形，点G，F分别在边CD和CB上，点E在正方形ABCD的内部．
  猜想证明：
  （1）DG和BF的位置关系是

  ，DG和BF的数量关系是

  ．
  （2）将正方形EFCG以C为中心顺时针方向旋转到图2所示位置，则（1）中的结论是否仍然成立？请说明理由．
  问题解决：
  （3）如图3，在正方形EFCG以C为中心顺时针旋转的过程中，当点E落在正方形ABCD的边AD上时，若CB=17，CF=13，则BF的长度是

  ．（请直接写出答案即可）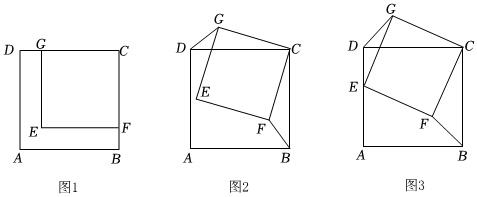
  
  组卷：65引用：3难度：0.1

  解析

• 23．如图，在平面直角坐标系中，抛物线

  y

  =

  1

  2

  x

  2

  +

  bx

  +

  c

  与直线AB交于点A（0，-4），B（4，0）．点P是直线AB下方抛物线上的一动点．
  （1）求该抛物线的函数表达式；
  （2）过点P作x轴的平行线交AB于点C，过点P作y轴的平行线交x轴于点D，求PC+PD的最大值及此时点P的坐标；
  （3）连接PA、PB，是否存在点P，使得线段PC把△PAB的面积分成1：3两部分，如果存在，请求出点P的坐标；如果不存在，请说明理由．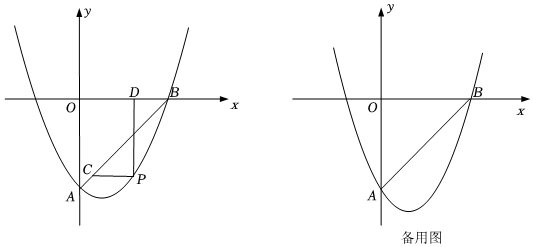
  组卷：481引用：3难度：0.3

  解析