2023-2024学年江苏省苏州市工业园区星海实验中学九年级（上）月考数学试卷（10月份）
发布：2024/9/17 0:0:8
一、单选题（本大题共8小题，每小题3分，共24分）
-
1．下列方程为一元二次方程的是（ ）
组卷：106引用：7难度：0.7 -
2．用配方法解方程x2-10x+9=0时，配方所得的方程为（ ）
组卷：195引用：5难度：0.7 -
3．一元二次方程x（x-2）+x-2=0的根为（ ）
组卷：159引用：5难度：0.7 -
4．为解决群众看病贵的问题，有关部门决定降低药价，某种药品原价为289元，在连续进行两次降价后价格调整为256元，设平均每次降价的百分率为x,则下面所列方程正确的是（ ）
组卷：241引用：5难度：0.5 -
5．若关于x的一元二次方程（k-5）x2-2x+2=0有实数根，则整数k的最大值为（ ）
组卷：2862引用：18难度：0.7 -
6．已知a＜-1，点（a-1，y1），（a,y2），（a+1，y3）都在函数y=3x2的图象上，则（ ）
组卷：190引用：1难度：0.7 -
7．已知关于x的方程ax2+bx+1=0的两根为x1=1，x2=2，则方程a（x+2）2+b（x+2）+1=0的两根之和为（ ）
组卷：299引用：3难度：0.5 -
8．已知等腰三角形的一边长为4，另外两边长是关于x的方程kx2-（k+8）x+8=0的两个根，则这个等腰三角形的周长为（ ）
组卷：337引用：3难度：0.5
二、填空题（本大题共8小题，每小题3分，共24分）
-
9．如果关于x的方程（m-3）
-x+3=0是一元二次方程，那么m的值为 ．xm2-7组卷：1099引用：11难度：0.7
三、简答题（本大题共11小题，共82分）
-
26．综合与实践
如图1，某兴趣小组计划开垦一个面积为8m2的矩形地块ABCD种植农作物，地块一边靠墙，另外三边用木栏围住，木栏总长为a m.
【问题提出】
小组同学提出这样一个问题：若a=10，能否围出矩形地块？
【问题探究】
小颖尝试从“函数图象”的角度解决这个问题：
设AB为x m,BC为y m.由矩形地块面积为8m2，得到xy=8，满足条件的（x,y）可看成是反比例函数y=的图象在第一象限内点的坐标；木栏总长为10m,得到2x+y=10，满足条件的（x,y）可看成一次函数y=-2x+10的图象在第一象限内点的坐标，同时满足这两个条件的（x,y）就可以看成两个函数图象交点的坐标．8x
如图2，反比例函数y=（x＞0）的图象与直线l1：y=-2x+10的交点坐标为（1，8）和 ，因此，木栏总长为10m时，能围出矩形地块，分别为：AB=1m,BC=8m；或AB=m,BC=m.8x
（1）根据小颖的分析思路，完成上面的填空；
【类比探究】
（2）若a=6，能否围出矩形地块？请仿照小颖的方法，在图2中画出一次函数图象并说明理由；
【问题延伸】
当木栏总长为a m时，小颖建立了一次函数y=-2x+a.发现直线y=-2x+a可以看成是直线y=-2x通过平移得到的，在平移过程中，当过点（2，4）时，直线y=-2x+a与反比例函数y=（x＞0）的图象有唯一交点．8x
（3）请在图2中画出直线y=-2x+a过点（2，4）时的图象，并求出a的值；
【拓展应用】
小颖从以上探究中发现“能否围成矩形地块问题”可以转化为“y=-2x+a与y=图象在第一象限内交点的存在问题”．8x
（4）若要围出满足条件的矩形地块，且AB和BC的长均不小于1m,请直接写出a的取值范围．
组卷：4666引用：14难度：0.6 -
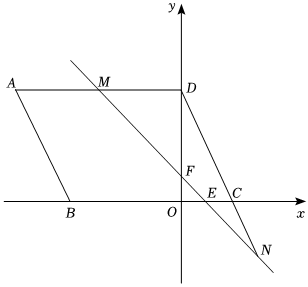27．如图，在平面直角坐标系中，▱ABCD的顶点B，C在x轴上，D在y轴上，OB，OC的长是方程x2-6x+8=0的两个根（OB＞OC）．请解答下列问题：
（1）求点B的坐标；
（2）若OD：OC=2：1，直线y=-x+1分别交x轴、y轴、AD于点E，F，M，且M是AD的中点，直线EF交DC延长线于点N，点P在y轴上，在直线EF上是否存在点Q，使△NPQ是腰长为5的等腰三角形？若存在，请直接写出等腰三角形的个数和其中两个点Q的坐标；若不存在，请说明理由．组卷：4引用：1难度：0.5
