2022-2023学年四川省宜宾市南溪区八年级(上)期中数学试卷
发布:2024/9/7 2:0:9
一、单选题(本大题共12个小题,每小题4分,共48分).在每小题给出的四个选项中,只有一项是符合题目要求的
-
1.在0,0.2,3π,
,6.1010010001…(相邻两个1之间0的个数依次加1),227,38中,无理数有( )个.7组卷:41引用:3难度:0.8 -
2.下列各等式中,从左到右的变形是因式分解的是( )
组卷:50引用:1难度:0.8 -
3.计算(-
)2023×(72)2022的结果是( )27组卷:145引用:2难度:0.7 -
4.下列运算中,结果正确的是( )
组卷:842引用:8难度:0.8 -
5.若约定a⊗b=10a×10b,如2⊗3=102×103=105,则3⊗4等于( )
组卷:604引用:3难度:0.9 -
6.已知
+|b-1|=0.那么(a+b)2023的值为( )a+2组卷:1445引用:11难度:0.7 -
7.化简
的结果是( )4组卷:93引用:7难度:0.8 -
8.如果(x+m)(x-3)中不含x的项,则m的值是( )
组卷:68引用:9难度:0.9
三、解答题(共78分)
-
24.观察如图1所示图形,每个小正方形的边长为1.
(1)则图中阴影部分的面积是 ,边长是 ,并在数轴上(图2)准确地作出表示阴影正方形边长的点.
(2)已知x为阴影正方形边长的小数部分,y为的整数部分,15
求:①x,y的值:
②(x+y)2的算术平方根.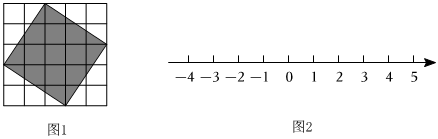 组卷:454引用:3难度:0.5
组卷:454引用:3难度:0.5 -
 25.若x满足(9-x)(x-4)=4,求(9-x)2+(x-4)2的值.
25.若x满足(9-x)(x-4)=4,求(9-x)2+(x-4)2的值.
解:设9-x=a,x-4=b,则(9-x)(x-4)=ab=4,a+b=(9-x)+(x-4)=5,
∴(9-x)2+(x-4)2=a2+b2=(a+b)2-2ab=52-2×4=17.
请仿照上面的方法求解下面问题:
(1)若x满足(x-10)(x-20)=15,求(x-10)2+(x-20)2的值;
(2)若x满足(x-2021)2+(x-2022)2=33,求(x-2021)(x-2022)的值;
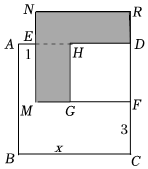
(3)已知正方形ABCD的边长为x,E,F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是48,分别以MF、DF为边长作正方形MFRN和正方形GFDH,求阴影部分的面积.组卷:578引用:4难度:0.6


