当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省徐州市高二（下）期末数学试卷

发布：2024/7/12 8:0:9

1．已知集合A={x|-3＜x＜1}，B={x||x|≥2}，则（　　）
A．A∩B={x|-3≤x≤-2} B．A∪∁_RB={x|-2＜x＜1}
C．A∩B={x|-3＜x＜-2} D．A∪∁_RB={x|-3＜x＜2}
组卷：69引用：2难度：0.7
解析
2．已知A，B，C，D四点在平面α内，且任意三点都不共线，点P在α外，且满足
AP
+
BP
-
3
CP
+
z
DP
=
0
，则z=（　　）
A．0 B．1 C．2 D．3
组卷：114引用：6难度：0.7
解析
3．3名男生和2名女生排成一排，其中女生甲不排两端的不同排法有（　　）
A．36种 B．48种 C．72种 D．120种
组卷：122引用：4难度：0.6
解析
4．某射手每次射击击中目标的概率是0.6，且各次射击的结果互不影响，则该射手射击30次恰有18次击中目标的概率为（　　）
A．0.6¹⁸×0.4¹² B．
C
18
30
0
．
6
18
×
0
．
4
12
C．
C
18
30
0
．
4
18
×
0
．
6
12
D．
C
18
30
0
．
6
18
组卷：300引用：3难度：0.8
解析
5．若a＞0，b＞0，则a+b≥6的一个充分条件是（　　）
A．
a
b
=
16
B．ab=9 C．a²+b²=4 D．
1
a
+
1
b
=
1
组卷：66引用：2难度：0.7
解析
6．已知集合A={a,b,c,d,e}，B={1，2，3}，f：A→B为从A到B的函数，且f（x）=1有两个不同的实数根，则这样的函数个数为（　　）
A．50 B．60 C．70 D．80
组卷：114引用：2难度：0.8
解析
7．已知a=2.57，
b
=
e
+
1
，c=1.1¹⁰，则（　　）
A．a＜c＜b B．a＜b＜c C．b＜a＜c D．c＜b＜a
组卷：67引用：2难度：0.5
解析

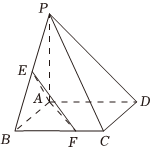21．如图，在四棱锥P-ABCD中，底面ABCD为正方形，PA⊥底面ABCD，PA=AB=2，E，F分别在棱PB，BC上．
（1）当E为棱PB中点时，求证：AE⊥EF；
（2）当F为棱BC中点时，求平面AEF与平面PDC所成的二面角余弦值的最大值．
组卷：129引用：3难度：0.6
解析
22．已知函数f（x）=a|x-1|+x|x-a|-
1
2
（a＞0）有三个零点x₁，x₂，x₃（x₁＜x₂＜x₃）．
（1）求实数a的取值范围；
（2）若λx₁＞x₂x₃，求实数λ的取值范围．
组卷：105引用：1难度：0.2
解析

A．A∩B={x\|-3≤x≤-2}	B．A∪∁_RB={x\|-2＜x＜1}
C．A∩B={x\|-3＜x＜-2}	D．A∪∁_RB={x\|-3＜x＜2}

A．0.6¹⁸×0.4¹²	B． C 18 30 0 ． 6 18 × 0 ． 4 12
C． C 18 30 0 ． 4 18 × 0 ． 6 12	D． C 18 30 0 ． 6 18

1．已知集合A={x|-3＜x＜1}，B={x||x|≥2}，则（ ）