当前位置：试卷中心 > 试卷详情

2022-2023学年甘肃省武威九中、爱华育新学校等三校九年级（下）期中数学试卷

发布：2024/7/4 8:0:9

一、选择题。（本大题共10小题，每小题3分，共30分，每小题只有一个正确选项）。

1．同学们，我们是2023届学生，这个数字2023的相反数是（　　）
A．2023 B．
1
2023
C．-2023 D．
-
1
2023
组卷：681引用：6难度：0.5
解析
2．中国空间站俯瞰地球的高度约为400000米，将400000用科学记数法表示应为（　　）
A．4×10⁵ B．4×10⁶ C．40×10⁴ D．0.4×10⁶
组卷：180引用：8难度：0.7
解析
3．已知三角形的两边长分别为5cm和8cm,则第三边的长可以是（　　）
A．2cm B．3cm C．6cm D．13cm
组卷：1613引用：40难度：0.8
解析
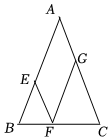4．如图，在△ABC中，AB=AC=8．点E，F，G分别在边AB，BC，AC上，EF∥AC，GF∥AB，则四边形AEFG的周长是（　　）
A．32 B．24 C．16 D．8
组卷：1081引用：6难度：0.5
解析
5．如图是反比例函数y=
1
x
的图象，点A（x,y）是反比例函数图象上任意一点，过点A作AB⊥x轴于点B，连接OA，则△AOB的面积是（　　）
A．1 B．
1
2
C．2 D．
3
2
组卷：1163引用：9难度：0.5
解析
6．下列运算正确的是（　　）
A．
2
+
3
=
5
B．3⁰=0
C．（-2a）³=-8a³ D．a⁶÷a³=a²
组卷：520引用：8难度：0.7
解析
7．若一次函数y=2x+1的图象经过点（-3，y₁），（4，y₂），则y₁与y₂的大小关系是（　　）
A．y₁＜y₂ B．y₁＞y₂ C．y₁≤y₂ D．y₁≥y₂
组卷：2604引用：24难度：0.6
解析
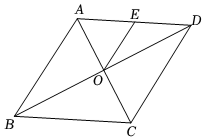8．如图，菱形ABCD的对角线AC与BD相交于点O，E为AD的中点，连接OE，∠ABC=60°，BD=4
3
，则OE=（　　）
A．4 B．2
3
C．2 D．
3
组卷：1470引用：15难度：0.7
解析
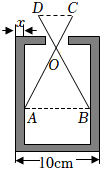9．如图，某零件的外径为10cm,用一个交叉卡钳（两条尺长AC和BD相等）可测量零件的内孔直径AB．如果OA：OC=OB：OD=3，且量得CD=3cm,则零件的厚度x为（　　）
A．0.3cm B．0.5cm C．0.7cm D．1cm
组卷：2179引用：14难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本题共5小题，共40分，解答时，应写出必要的文字说明、证明过程或演算步骤）。

27．【问题情境】：数学活动课上，老师出示了一个问题：如图1，在正方形ABCD中，E是BC的中点，AE⊥EP，EP与正方形的外角∠DCG的平分线交于P点，试猜想AE与EP的数量关系，并加以证明．
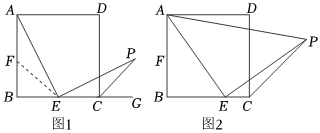
（1）【思考尝试】：有同学发现，取AB的中点F，连接EF可以解决这个问题．请在图1中补全图形，解答老师提出的问题；
（2）【实践探究】：有同学受此问题启发，逆向思考这个题目，并提出新的问题：如图2，在正方形ABCD中，E为BC边上一动点（点E与B不重合），当△AEP是等腰直角三角形，∠AEP=90°，连接CP，可以求出∠DCP的大小，请你思考并解答这个问题．
组卷：84引用：2难度：0.4
解析
28．如图1，已知在平面直角坐标系xOy中，四边形OABC是边长为3的正方形，其中顶点A，C分别在x轴的正半轴和y轴的正半轴上，抛物线y=-x²+bx+c经过A，C两点，与x轴交于另一个点D．

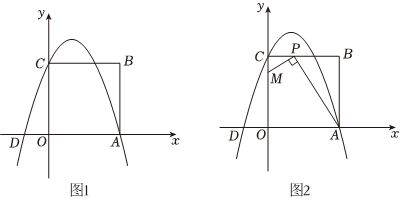
（1）①求b,c的值；
②在平面内是否存在点Q，使得以点A、C、D、Q为顶点的四边形是平行四边形？若存在，请直接写出点Q的坐标；若不存在，请说明理由；
（2）若点P是边BC上的一个动点，连接AP，过点P作PM⊥AP，交y轴于点M（如图2所示），当点P在BC上运动时，点M也随之运动，设BP=m,CM=n,试用含m的代数式表示n,并求出n的最大值．
组卷：72引用：2难度：0.3
解析