2022-2023学年北京市门头沟区八年级（下）期末数学试卷

一、选择题（本题共16分，每小题2分）

• 1．如果点P的坐标是（-4，2），那么点P在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：59引用：2难度：0.9

  解析

• 2．下列图形，既是轴对称图形，又是中心对称图形的是（　　）

  A． 等腰三角形

  B． 等边三角形

  C． 平行四边形

  D． 矩形
  组卷：142引用：3难度：0.8

  解析

• 3．如果一个多边形的内角和与外角和相等，那么这个多边形的边数是（　　）

  A．3

  B．4

  C．5

  D．6
  组卷：570引用：10难度：0.8

  解析

• 4．关于x的方程（m-1）

  x

  m

  2

  +

  1

  +x-3=0是一元二次方程，则（　　）

  A．m=-1

  B．m=1

  C．m=±1

  D．m=2
  组卷：383引用：2难度：0.9

  解析

• 5．下列图象中，y是x的函数的是（　　）

  A．

  B．

  C．

  D．
  组卷：149引用：1难度：0.9

  解析

• 6．某工厂2021年生产某种机械5000台，研发生产技术后，预计2023年生产该种机械6600台．设生产该种机械的年平均增长率为x,下面所列方程正确的是（　　）

  A．5000（1+x）2=6600

  B．5000x2=6600

  C．6600（1-x）2=5000

  D．5000（1+x）+5000（1+x）2=6600
  组卷：295引用：3难度：0.5

  解析

• 7．下列命题是判断一个四边形是平行四边形的语句，其中错误的是（　　）

  A．一组对边平行且相等

  B．两组对边分别相等

  C．对角线互相平分

  D．一组对边相等另一组对边平行
  组卷：45引用：1难度：0.6

  解析

• 8．在一次外语测验中，某年级人数相同的两个班的成绩统计如下表：
  

  班级	平均数	中位数	方差
  1班	82.5	85.5	40.25
  2班	82.5	80.5	35.06

  小亮同学对此做出如下评估：
  ①这次外语测验成绩两个班的平均水平相同：
  ②1班学生中成绩优秀（85分及以上）的多；
  ③2班学生的成绩比较整齐，分化较小．
  上述评估正确的是（　　）

  A．①

  B．①②

  C．①③

  D．①②③
  组卷：102引用：1难度：0.7

  解析

二、填空题（本题共16分，每小题2分）

• 9．函数y=

  1

  x

  -

  3

  中，自变量x的取值范围是

  ．
  组卷：1151引用：192难度：0.9

  解析

三、解答题（本题共68分，第17～20题每小题5分，第21题6分、第22题5分、第23、24题每小题5分，第25题5分，第26题6分，第27～28题每小题5分）

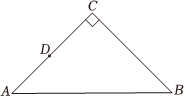• 27．如图，在等腰直角△ABC中，∠C=90°，点D是AC边上一点，作射线BD，过点A作AE⊥BD于点E，连接AE．
  （1）根据题意补全图形；
  （2）求证：∠EAD=∠DBC；
  （3）用等式表示线段EA，EB，EC之间的等量关系，并证明．
  组卷：316引用：1难度：0.2

  解析

• 28．我们给出如下定义：两个图形G₁和G₂对于G₁上的任意一点P（x₁，y₁）与G₂上的任意一点Q（x₂，y₂），如果线段PQ的长度最短，我们就称线段PQ为“理想距离”．
  （1）如图1，点P在线段AB（A（1，0），B（3，0））上，点Q在线段CD上，如果PQ为理想距离，那么PQ的长为

  ；
  （2）有射线EF（E（4，0），F（0，4））和线段AB，点P在线段AB上，点Q在射线EF上：
  ①如图2，当A（1，0），B（3，0）时，画出理想距离的示意图，PQ的长为

  ；
  ②如图3，保持线段AB在x轴上（点A在点B的左侧），且AB为2个单位长度，A（m,0），理想距离PQ的长满足

  0

  ≤

  PQ

  ≤

  2

  ，画出示意图，写出m的取值范围．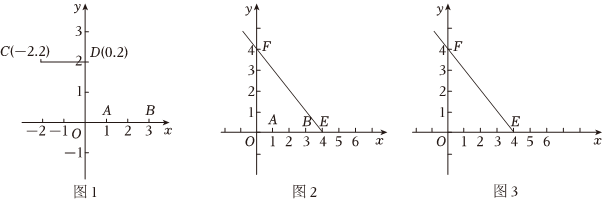
  
  组卷：599引用：4难度：0.2

  解析