2022-2023学年福建省泉州市永春县汤城中学九年级（上）第二次月考数学试卷

一、选择题（本大题共10小题，每小题4分，共40分）

• 1．若二次根式

  5

  -

  x

  有意义，则x的取值范围是（　　）

  A．x≥0

  B．x＞0

  C．x≤5

  D．x＜5
  组卷：913引用：13难度：0.8

  解析

• 2．若

  a

  2

  =

  b

  3

  ，则

  a

  +

  b

  b

  的值为（　　）

  A． 1 3

  B． 2 3

  C． 5 3

  D． 3 5
  组卷：728引用：8难度：0.9

  解析

• 3．“购买1张彩票，中奖”这个事件是（　　）

  A．不可能事件

  B．必然事件

  C．确定性事件

  D．随机事件
  组卷：266引用：7难度：0.8

  解析

• 4．若关于x的方程（a+1）x²+2x-1=0是一元二次方程，则a的取值范围是（　　）

  A．a≠-1

  B．a＞-1

  C．a＜-1

  D．a≠0
  组卷：461引用：12难度：0.9

  解析

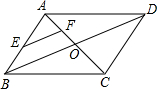• 5．如图，在▱ABCD中，对角线AC，BD相交于点O，点E，F分别是AB，AO的中点，连接EF，若EF=2，则BD的长为（　　）

  A．10

  B．8

  C．6

  D．4
  组卷：686引用：11难度：0.5

  解析

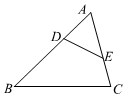• 6．如图，D，E分别是△ABC的边AB，AC上的点，添加下列条件仍不能判定△ADE与△ABC相似（　　）

  A．DE∥BC

  B．∠ADE=∠ACB

  C． AD AC = AE AB

  D． AD AB = DE BC
  组卷：378引用：6难度：0.7

  解析

• 7．已知α，β是方程x²+2020x+1=0的两个根，则（1+2022α+α²）（1+2022β+β²）的值为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：50引用：2难度：0.6

  解析

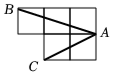• 8．如图中的每个小正方形的边长均相等，则sin∠BAC的值为（　　）

  A．1

  B． 2 2

  C． 3 2

  D． 2 3
  组卷：677引用：4难度：0.5

  解析

三、解答题（共86分）

• 24．如图，在矩形ABCD中，AB=6，BC=8，点E是AD边上的动点，将矩形ABCD沿BE折叠，点A落在点A'处，连接A'C、BD．
  
  （1）如图1，求证：∠DEA'=2∠ABE；
  （2）如图2，若点A'恰好落在BD上，求证：AB=2AE；
  （3）若AE=2，求S_△A'CB的值；
  （4）点E在AD边上运动的过程中，∠A'CB的度数是否存在最大值？若存在，求出此时线段AE的长；若不存在，请说明理由．
  组卷：49引用：2难度：0.2

  解析

• 25．如图1，在平面直角坐标系中，抛物线y=x²+bx+c与x轴交于点A、B（点B在点A右侧），与y轴交于点C，且OC=OB=3OA=3，E是第四象限内抛物线上的动点．
  （1）求抛物线的解析式；
  （2）连接OE交BC于点F，当S_△CEF：S_△OCF的值最大时，求点E的坐标；
  （3）在（2）的条件下：当S_△CEF：S_△OCF的值最大时，如图2，过点E作ED⊥x轴于点D，交BC于点M，在x轴上是否存在这样的点P，使得以点M，B，P为顶点的三角形是等腰三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由．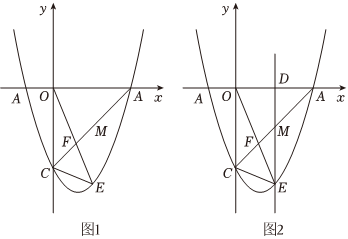
  
  组卷：21引用：2难度：0.5

  解析