2022-2023学年山东省枣庄市山亭区八年级（下）期末数学试卷
发布：2024/6/27 8:0:9
一、选择题：本大题共10小题，每小题3分，满分30分，在每小题给出的四个选项中，只有一项是正确的。
-
1．窗棂即窗格（窗里面的横的、竖的或斜的格）是中国传统木构建筑的框架结构设计，窗棂上雕刻有线槽和各种花纹，构成种类繁多的优美图案．下列表示我国古代窗棂样式结构图案中，既是轴对称图形又是中心对称图形的是（ ）
组卷：265引用：7难度：0.9 -
2．下列代数式是分式的是（ ）
组卷：298引用：3难度：0.9 -
3．已知两个不等式的解集在数轴上如图表示，那么这个解集为（ ）组卷：640引用：5难度：0.8 -
4．如图，直角坐标系中，Rt△AOB的顶点A在x轴上，∠B=90°，OA=5，OB=3，现将△AOB绕原点O按顺时针方向旋转，得到△DOC，且点C在x轴上，则点D的坐标是（ ）组卷：139引用：6难度：0.9 -
5．照相机成像应用了一个重要原理，用公式
=1f+1u（v≠f）表示，其中f表示照相机镜头的焦距，u表示物体到镜头的距离，v表示胶片（像）到镜头的距离．已知f,v,则u=（ ）1v组卷：2460引用：24难度：0.8 -
6．如图，在△ABC中，AB=AC，CE是△ACB的角平分线，若∠A=50°，则∠AEC的度数是（ ）组卷：351引用：2难度：0.7 -
7．依据所标数据，下列一定为平行四边形的是（ ）
组卷：722引用：6难度：0.7 -
8．化简
的结果为（ ）a2a-1-1-2a1-a组卷：3208引用：39难度：0.9
三、解答题：本大题共8小题，满分72分，解答时，要写出必要的文字说明、证明过程或演算步骤。
-
23．阅读两位同学的探究交流活动过程：
a.小明在做分式运算时发现如下一个等式，并对它进行了证明．；①x+2x+3-x+1x+2=1x+2-1x+3
b.小明尝试写出了符合这个特征的其他几个等式：；②x+3x+4-x+2x+3=1x+3-1x+4；③x+4x+5-x+3x+4=1x+4-1x+5；④x+5x+6-x+4x+5=1x+5-1x+6
…
c.小明邀请同学小亮根据上述规律写出第⑤个等式和第n个等式（用含n的式子表示，n为正整数）；
d.小亮对第n个等式进行了证明．
解答下列问题：
（1）第⑤个等式是 ；
（2）第n个等式是 ；
（3）请你证明第n个等式成立．组卷：959引用：4难度：0.5 -
24．如图（1），大正方形的面积可以表示为（a+b）2，同时大正方形的面积也可以表示成两个小正方形面积与两个长方形的面积之和，即a2+2ab+b2．同一图形（大正方形）的面积，用两种不同的方法求得的结果应该相等，从而验证了完全平方公式：
（a+b）2=a2+2ab+b2．
把这种“同一图形的面积，用两种不同的方法求出的结果相等，从而构建等式，根据等式解决相关问题”的方法称为“面积法”．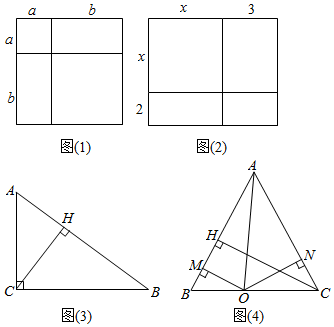
（1）用上述“面积法”，通过如图（2）中图形的面积关系，直接写出一个多项式进行因式分解的等式：．
（2）如图（3），Rt△ABC中，∠C=90°，CA=3，CB=4，CH是斜边AB边上的高．用上述“面积法”求CH的长；
（3）如图（4），等腰△ABC中，AB=AC，点O为底边BC上任意一点，OM⊥AB，ON⊥AC，CH⊥AB，垂足分别为点M，N，H，连接AO，用上述“面积法”求证：OM+ON=CH．组卷：685引用：5难度：0.5
