2022-2023学年浙江省宁波市余姚市姚江教共体九年级（上）第一次联考数学试卷

一、选择题（每题4分，共40分）

• 1．一个袋子中有7只黑球，6只黄球，5只白球，一次性取出12只球，其中出现黑球是（　　）

  A．不可能事件	B．必然事件
  C．随机事件	D．以上说法均不对
  组卷：30引用：3难度：0.9

  解析

• 2．⊙O内有一点P，过点P的所有弦中，最长的为10，最短的为8，则OP的长为（　　）

  A．6

  B．5

  C．4

  D．3
  组卷：108引用：2难度：0.7

  解析

• 3．已知点A（1，y₁），B（2

  2

  ，y₂），C（4，y₃）在二次函数y=x²-6x+c的图象上，则y₁，y₂，y₃的大小关系是（　　）

  A．y1＜y2＜y 3

  B．y2＜y3＜y 1

  C．y3＜y2＜y1

  D．y1＜y3＜y2
  组卷：637引用：3难度：0.5

  解析

• 4．已知实数a,b,c满足：a＜0，a-b+c＞0，则一定有（　　）

  A．b2-4ac＞0

  B．b2-4ac≥0

  C．b2-4ac≤0

  D．b2-4ac＜0
  组卷：460引用：16难度：0.7

  解析

• 5．小明利用测角仪和旗杆的拉绳测量学校旗杆的高度．如图，旗杆PA的高度与拉绳PB的长度相等．小明将PB拉到PB′的位置，测得∠PB′C=α（B′C为水平线），测角仪B′D的高度为1米，则旗杆PA的高度为（　　）

  A． 1 1 - sinα

  B． 1 1 + sinα

  C． 1 1 - cosα

  D． 1 1 + cosα
  组卷：3259引用：28难度：0.7

  解析

• 6．如图，将一张直角三角形纸片沿虚线剪成甲、乙、丙三块，其中甲、丙为梯形，乙为三角形．根据图中标示的边长数据，比较甲、乙、丙的面积大小，下列判断何者正确？（　　）
  

  A．甲＞乙，乙＞丙	B．甲＞乙，乙＜丙
  C．甲＜乙，乙＞丙	D．甲＜乙，乙＜丙
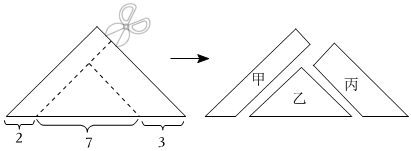  组卷：420引用：63难度：0.5

  解析

• 7．如图，△ABC中，∠A、∠B、∠C所对的三边分别记为a,b,c,O是△ABC的外心，OD⊥BC，OE⊥AC，OF⊥AB，则OD：OE：OF=（　　）

  A．a：b：c	B． 1 a ： 1 b ： 1 c
  C．cosA：cosB：cosC	D．sinA：sinB：sinC
  组卷：1168引用：16难度：0.9

  解析

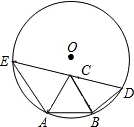• 8．已知AB是半径为1的圆O的一条弦，且AB=a＜1，以AB为一边在圆O内作正△ABC，点D为圆O上不同于点A的一点，且DB=AB=a,DC的延长线交圆O于点E，则AE的长为（　　）

  A． 5 2 a

  B．1

  C． 3 2

  D．a
  组卷：2698引用：23难度：0.5

  解析

三、解答题（本大题有8小题，共80分）

• 23．如图，在平面直角坐标系中，抛物线

  y

  =

  1

  4

  x

  2

  -

  3

  2

  x

  -

  4

  ，y与x轴交于A，B两点，与y轴交于点C．
  （1）直接写出点A、B、C的坐标；
  （2）直接写出△ABC的重心点M的坐标；
  （3）坐标系中存在点N（n,6），且∠ANB=45°，请你推导计算出n的值；
  （4）如图2．若点P在以点O为圆心，OA长为半径作的圆上，连接BP、CP，请你直接写出

  1

  2

  CP

  +

  BP

  的最小值．
  组卷：39引用：2难度：0.5

  解析

• 24．对于半径为r的⊙P及一个正方形给出如下定义：若⊙P上存在到此正方形四条边距离都相等的点，则称⊙P是该正方形的“等距圆”．如图1，在平面直角坐标系xOy中，正方形ABCD的顶点A的坐标为（2，4），顶点C、D在x轴上，且点C在点D的左侧．
  （1）当r=4

  2

  时，
  ①在P₁（0，-3），P₂（4，6），P₃（4

  2

  ，2）中可以成为正方形ABCD的“等距圆”的圆心的是

  ；
  ②若点P在直线y=-x+2上，且⊙P是正方形ABCD的“等距圆”，则点P的坐标为

  ；
  （2）如图2，在正方形ABCD所在平面直角坐标系xOy中，正方形EFGH的顶点F的坐标为（6，2），顶点E、H在y轴上，且点H在点E的上方．
  ①若⊙P同时为上述两个正方形的“等距圆”，且与BC所在直线相切，求⊙P在y轴上截得的弦长；
  ②将正方形ABCD绕着点D旋转一周，在旋转的过程中，线段HF上没有一个点能成为它的“等距圆”的圆心，则r的取值范围是

  ．
  
  组卷：160引用：2难度：0.3

  解析