2023年福建省厦门外国语学校中考数学二模试卷
发布:2024/6/17 8:0:9
一.选择题:本题共10小题,每小题4分,共40分.
-
1.下列数中,最小的数是( )
组卷:86引用:2难度:0.8 -
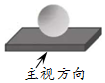 2.如图是由一个长方体和一个球组成的几何体,它的主视图是( )组卷:1094引用:27难度:0.9
2.如图是由一个长方体和一个球组成的几何体,它的主视图是( )组卷:1094引用:27难度:0.9 -
3.我国的“天问一号”火星探测器成功着陆火星,据测算,地球到火星的最近距离约为55000000千米,数据55000000用科学记数法表示为( )
组卷:92引用:5难度:0.9 -
4.下列计算结果是a5的是( )
组卷:207引用:8难度:0.8 -
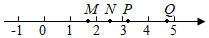 5.如图,数轴上表示实数的点可能是( )10组卷:553引用:9难度:0.6
5.如图,数轴上表示实数的点可能是( )10组卷:553引用:9难度:0.6 -
6.下列命题中是假命题的是( )
组卷:44引用:1难度:0.5 -
 7.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则的长( )ˆAC组卷:6592引用:82难度:0.9
7.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则的长( )ˆAC组卷:6592引用:82难度:0.9 -
8.《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安,今乙发已先二日,甲乃发长安.问几何日相逢?译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙先出发2日,甲才从长安出发.问甲乙经过多少日相逢?若设甲经过x日相逢,则可列方程为( )
组卷:202引用:3难度:0.5
三.解答题:本题共9小题,共86分.
-
24.【课本再现】
(1)如图1,正方形ABCD的对角线相交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长都为1,四边形OEBF为两个正方形重叠部分,正方形A1B1C1O可绕点O转动.则下列结论正确的是 (填序号即可).
①△AEO≌△BFO;
②OE=OF;
③四边形OEBF的面积总等于;14
④连接EF,总有AE2+CF2=EF2.
【类比迁移】
(2)如图2,矩形ABCD的中心O是矩形A1B1C1O的一个顶点,A1O与边AB相交于点E,C1O与边CB相交于点F,连接EF,矩形A1B1C1O可绕着点O旋转,猜想AE,CF,EF之间的数量关系,并进行证明;
【拓展应用】
(3)如图3,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,直角∠EDF的顶点D在边AB的中点处,它的两条边DE和DF分别与直线AC,BC相交于点E,F,∠EDF可绕着点D旋转,当AE=2cm时,求线段EF的长度.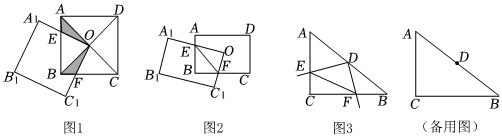 组卷:1476引用:13难度:0.1
组卷:1476引用:13难度:0.1 -
25.如图,抛物线
过点A(6,0),点B是抛物线的顶点,点D是x轴上方抛物线上的一点,连接OB,OD.y=ax2+23x(a≠0)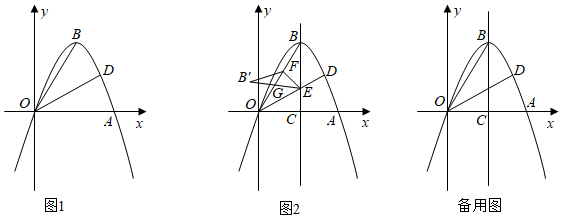
(1)求抛物线的解析式.
(2)如图1,当∠BOD=30°时,求点D的纵坐标;
(3)如图2,在(2)的条件下,抛物线的对称轴交x轴于点C,交线段OD于点E,点F是线段OB上的动点(点F不与点O和点B重合)连接EF,将△BEF沿EF折叠,点B的对应点为点B',△EFB'与△OBE的重叠部分为△EFG,在第一象限内是否存在一点H,使以点E,F,G,H为顶点的四边形是矩形?若存在,请求出点H的坐标,若不存在,请说明理由.组卷:320引用:2难度:0.3


