2022-2023学年山东省滨州市高新高级中学高一(下)期中数学试卷
发布:2024/5/21 8:0:9
一、单选题(每小题5分,共8小题,共40分)
-
1.设z=3-2i,则在复平面内z对应的点位于( )
组卷:22引用:5难度:0.9 -
2.已知直线a,b,平面α,β,且a⊂α,b⊂β,α∥β,则下列结论一定成立的是( )
组卷:62引用:2难度:0.6 -
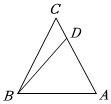 3.如图,在△ABC中,AD=2DC,若,BA=a,则BC=b=( )BD组卷:326引用:5难度:0.8
3.如图,在△ABC中,AD=2DC,若,BA=a,则BC=b=( )BD组卷:326引用:5难度:0.8 -
4.在△ABC中,角A,B,C所对的边分别是a,b,c,若A=60°,B=45°,a=3,则b=( )
组卷:456引用:8难度:0.7 -
5.已知向量
=(4,2),向量a=(x,3),且b∥a,则x=( )b组卷:560引用:27难度:0.9 -
6.已知圆锥的底面半径为1,高为
,则圆锥的侧面积为( )22组卷:259引用:5难度:0.8 -
7.已知向量
=(-1,2),a=(1,1),则b在a上的投影向量为( )b组卷:503引用:6难度:0.8
四、解答题(共6小题,17题10分,18-22题每小题10分,共70分)
-
21.在△ABC中,角A,B,C所对的边分别为a,b,c.向量
,m=(3a,b),且n=(sinA,cosB).m∥n
(Ⅰ)求B的值;
(Ⅱ)若a=2,b=,求△ABC的面积.7组卷:176引用:3难度:0.5 -
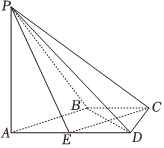 22.如图,在四棱锥P-ABCD中,AD∥BC,AD⊥DC,,E为棱AD的中点,PA⊥平面ABCD.BC=CD=12AD=2
22.如图,在四棱锥P-ABCD中,AD∥BC,AD⊥DC,,E为棱AD的中点,PA⊥平面ABCD.BC=CD=12AD=2
(1)证明:AB∥平面PCE;
(2)求证:平面PAB⊥平面PBD;
(3)若二面角P-CD-A的大小为45°,求直线AD与平面PBD所成角的正切值.组卷:362引用:6难度:0.5


