当前位置：试卷中心 > 试卷详情

2021-2022学年山东省青岛十九中高一（下）期中数学试卷

发布：2024/6/28 8:0:9

一、单项选择题。本大题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知复数z=1-2i,则z在复平面内对应的点关于虚轴对称的点是（　　）
A．（1，-2） B．（1，2） C．（-2，1） D．（-1，-2）
组卷：20引用：2难度：0.8
解析
2．sin46°cos16°-sin44°sin164°=（　　）
A．
-
1
2
B．
1
2
C．
3
2
D．
-
3
2
组卷：18引用：1难度：0.7
解析
3．某校为了解学生学习的情况，采用分层抽样的方法从高一2400人、高二2000人、高三n人中，抽取180人进行问卷调查．已知高二被抽取的人数为60人，那么高三被抽取的人数为（　　）
A．72 B．60 C．48 D．84
组卷：144引用：3难度：0.9
解析
4．已知sin（α-
π
4
）=
5
5
，则sin2α=（　　）
A．
4
5
B．
-
4
5
C．
3
5
D．
-
3
5
组卷：96引用：3难度：0.9
解析
5．在平行四边形ABCD中，|
AB
|=3，若
BA
|
BA
|
+
BC
|
BC
|
=
BD
|
BD
|
，则|
AC
|=（　　）
A．2
3
B．3
3
C．4
3
D．3
组卷：215引用：7难度：0.8
解析
6．某射击运动员7次的训练成绩分别为：86，88，90，89，88，87，85，则这7次成绩的第80百分位数为（　　）
A．88.5 B．89 C．91 D．89.5
组卷：353引用：8难度：0.7
解析
7．2021年11月，郑州二七罢工纪念塔入选全国职工爱国主义教育基地名单．某数学建模小组为测量塔的高度，获得了以下数据：甲同学在二七广场A地测得纪念塔顶D的仰角为45°，乙同学在二七广场B地测得纪念塔顶D的仰角为30°，塔底为C，（A，B，C在同一水平面上，DC⊥平面ABC），测得AB=63m,∠ACB=30°，则纪念塔的高CD为（　　）
A．40m B．63m C．
40
3
m D．
63
3
m
组卷：70引用：3难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题。本大题共6小题，第17题10分，18-22题每题12分，共70分.解答应写出文字说明，证明过程或演算步骤。

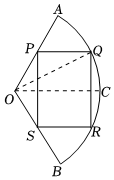21．今年2月底俄罗斯与乌克兰冲突爆发以来，大量的乌克兰人民离开故土开启了逃亡之路，截止3月底，联合国难民事务高级专员表示，乌克兰难民人数已经超过400万，其中大多数逃往波兰、匈牙利、摩尔多瓦、罗马尼亚和斯洛伐克等邻国．各邻国都在陆续建立难民收容所，波兰某地准备在一个废弃的汽车停车场，临时建一处形状为矩形的收容所供乌克兰难民所用．已知停车场是近似如图所示半径为50米，圆心角为
2
π
3
的扇形区域AOB，C为弧
ˆ
AB
的中点，设∠QOC=θ，
（1）用θ来表示矩形PQRS的面积f（θ），并指出θ的取值范围；
（2）θ为多少时，f（θ）取得最大值，并求出此最大值．
组卷：34引用：3难度：0.6
解析
22．已知函数
f
（
x
）
=
2
sin
（
x
+
π
3
）
．
（1）若不等式|f（x）-m|≤3对任意
x
∈
[
-
π
6
，
π
3
]
恒成立，求整数m的最大值；
（2）若函数
g
（
x
）
=
f
（
π
2
-
x
）
，将函数g（x）的图像上各点的横坐标缩短到原来的
1
2
倍（纵坐标不变），再向右平移
π
12
个单位，得到函数y=h（x）的图像，若关于x的方程
1
2
h
（
x
）
-
k
（
sinx
+
cosx
）
=
0
在
x
∈
[
-
π
12
，
5
π
12
]
上有解，求实数k的取值范围．
（参考公式：sin2x=2sinxcosx,
sinx
+
cosx
=
2
sin
（
x
+
π
4
）
）
组卷：229引用：3难度：0.5
解析