2022-2023学年江苏省南京市江宁区高新中学九年级（上）月考数学试卷（12月份）

一、选择题（每题2分，满分12分）

• 1．若一元二次方程（k-1）x²+3x+k²-1=0有一个解为x=0，则k为（　　）

  A．±1

  B．1

  C．-1

  D．0
  组卷：885引用：7难度：0.6

  解析

• 2．五名同学捐款数分别是5，3，6，5，10（单位：元），捐10元的同学后来又追加了10元．追加后的5个数据与之前的5个数据相比，集中趋势相同的是（　　）

  A．只有平均数	B．只有中位数
  C．只有众数	D．中位数和众数
  组卷：2278引用：28难度：0.5

  解析

• 3．在一个不透明的袋子里装有红球、黄球共20个，这些球除颜色外都相同．小明通过多次试验发现，摸出红球的频率稳定在0.25左右，则袋子中红球的个数最有可能是（　　）

  A．5

  B．10

  C．12

  D．15
  组卷：3030引用：52难度：0.7

  解析

• 4．设圆锥的底面圆半径为r,圆锥的母线长为l,满足2r+l=6，这样的圆锥的侧面积（　　）

  A．有最大值 9 4 π	B．有最小值 9 4 π
  C．有最大值 9 2 π	D．有最小值 9 2 π
  组卷：1944引用：8难度：0.7

  解析

• 5．如图，一枚圆形古钱币的中间是一个正方形孔，已知圆的直径与正方形的对角线之比为3：1，则圆的面积约为正方形面积的（　　）

  A．27倍

  B．14倍

  C．9倍

  D．3倍
  组卷：1630引用：5难度：0.6

  解析

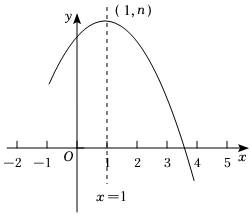• 6．如图所示是抛物线y=ax²+bx+c（a＜0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间，则下列结论：①a-b+c＞0；②3a+c＞0；③b²=4a（c-n）；④一元二次方程ax²+bx+c=n-2没有实数根．其中正确的结论个数是（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：1274引用：11难度：0.6

  解析

二、填空题（每小题2分，满分20分）

• 7．关于x的方程（x+1）²=9的根为

  ．
  组卷：29引用：1难度：0.7

  解析

• 8．将二次函数y=2x²-4x-1的图象沿着y轴翻折，所得到的图象对应的函数表达式是

  ．
  组卷：1467引用：4难度：0.6

  解析

三、解答题（满分74分）

• 25．【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积？
  【初步尝试】如图1，已知扇形OAB，请你用圆规和无刻度的直尺过圆心O作一条直线，使扇形的面积被这条直线平分；
  【问题联想】如图2，已知线段MN，请你用圆规和无刻度的直尺作一个以MN为斜边的等腰直角三角形MNP；
  【问题再解】如图3，已知扇形OAB，请你用圆规和无刻度的直尺作一条以点O为圆心的圆弧，使扇形的面积被这条圆弧平分．
  （友情提醒：以上作图均不写作法，但需保留作图痕迹）
  
  组卷：2957引用：16难度：0.5

  解析

• 26．【发现问题】
  小明在练习簿的横线上取点O为圆心，相邻横线的间距为半径画圆，然后半径依次增加一个间距画同心圆，描出了同心圆与横线的一些交点，如图1所示，他发现这些点的位置有一定的规律．
  【提出问题】
  小明通过观察，提出猜想：按此步骤继续画圆描点，所描的点都在某二次函数图象上．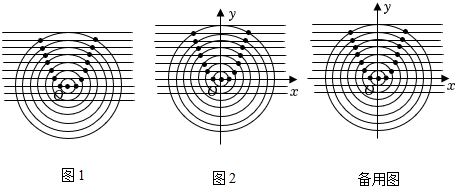
  
  【分析问题】
  小明利用已学知识和经验，以圆心O为原点，过点O的横线所在直线为x轴，过点O且垂直于横线的直线为y轴，相邻横线的间距为一个单位长度，建立平面直角坐标系，如图2所示．当所描的点在半径为5的同心圆上时，其坐标为

  ．
  【解决问题】
  请帮助小明验证他的猜想是否成立．
  【深度思考】
  小明继续思考：设点P（0，m），m为正整数，以OP为直径画⊙M，是否存在所描的点在⊙M上．若存在，求m的值；若不存在，说明理由．
  组卷：1876引用：7难度：0.4

  解析