2021-2022学年青岛青大附中八年级（下）期末数学试卷

一、选择题（本题满分24分，共有8道小题，每小题3分）

• 1．下列图案中是轴对称图形，但不是中心对称图形的有（　　）

  A．

  B．

  C．

  D．
  组卷：109引用：4难度：0.8

  解析

• 2．如图，在△ABC中，∠C=90°，∠B=15°，AB的垂直平分线交BC于D，交AB于E，若DB=10cm,则CD的长为（　　）cm
  ​

  A．10

  B．8

  C．5

  D． 5 3
  组卷：375引用：7难度：0.6

  解析

• 3．下列运算正确的是（　　）

  A． a a - b - b b - a = 1	B． m a - n b = m - n a - b
  C． b a - b + 1 a = 1 a	D． 2 a - b - a + b a 2 - b 2 = 1 a - b
  组卷：490引用：30难度：0.9

  解析

• 4．如图为小丽和小欧依序进入电梯时，电梯因超重而警示音响起的过程，且过程中没有其他人进出．
  
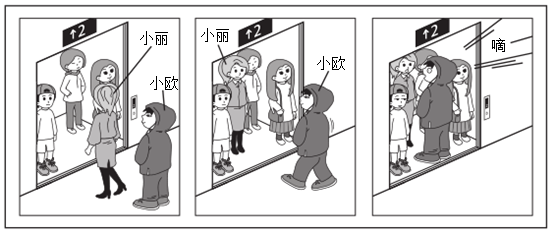
  已知当电梯乘载的重量超过300公斤时警示音响起，且小丽、小欧的重量分别为50公斤、70公斤．若小丽进入电梯前，电梯内已乘载的重量为x公斤，则所有满足题意的x可用下列哪一个不等式表示？（　　）

  A．180＜x≤250

  B．180＜x≤300

  C．230＜x≤250

  D．230＜x≤300
  组卷：974引用：14难度：0.5

  解析

• 5．当m=（　　）时，解分式方程

  x

  -

  5

  x

  -

  3

  =

  m

  3

  -

  x

  会出现增根（　　）

  A．5

  B．2

  C．-2

  D．3
  组卷：298引用：5难度：0.8

  解析

• 6．一个多边形的内角和是外角和的3倍，则这个多边形是（　　）

  A．四边形

  B．五边形

  C．六边形

  D．八边形
  组卷：294引用：5难度：0.5

  解析

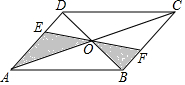• 7．如图，▱ABCD的对角线AC，BD相交于O，EF经过点O，分别交AD，BC于E，F，已知▱ABCD的面积是20cm²，则图中阴影部分的面积是（　　）

  A．12 cm2

  B．10 cm2

  C．8cm2

  D．5cm2
  组卷：1097引用：8难度：0.6

  解析

• 8．如图，四边形ABCD中，AD∥BC，AB≠BC．∠ABC=45°，AE⊥BC于点E，BF⊥AC于点F，交AE于点C．AD=BE，连接DG、CG．以下结论：①△BEG≌△AEC；②∠GAC=∠GCA；③DG=DC．其中正确的结论个数为（　　）
  ​

  A．0个

  B．1个

  C．2个

  D．3个
  组卷：203引用：2难度：0.5

  解析

四、解答题（本大题满分72分，共8道小题）

• 23．提出问题：有12个相同的长方体纸盒，它们的长、宽、高分别是4、3、5，现要用这12个纸盒搭成一个大长方体，怎样搭可使长方体的表面积最小？
  分析问题：对于这种问题，我们一般采用复杂问题简单化的策略，进行由特殊到一般的探究．
  探究一：我们以两个长、宽、高分别是4、3、5的长方体为例进行分析．我们发现，无论怎样放置这两个长方体纸盒，搭成的大长方体体积都不变，但是由于摆放位置的不同，它们的表面积会发生变化，经过操作，发现共有3种不同的摆放方式，如图所示．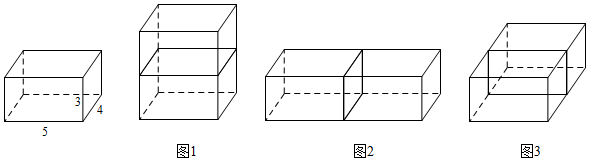
  
  （1）请计算图1、图2、图3中的拼成的新的大长方体的长、宽、高及其表面积，并填充下表：
  

  	长（cm）	宽（cm）	高（cm）	表面积（cm2）
  图1	5	4	6	148
  图2	10	4	3	164
  图3	5	8	3

  根据上表可知，表面积最小的是

  所示的长方体．（填“图1”、“图2”、“图3”）
  探究二：有4个相同的长方体纸盒，它们的长、宽、高分别是5、4、3，现要用这4个纸盒搭成一个大长方体，怎样搭可使长方体的表面积最小？
  先画出各种摆法的示意图，再根据各自的表面积得到最小摆法，是一种常规的方法，但比较耗时，也不方便，可以按照下列思路考虑：
  在图1的基础上继续摆，要使表面积小，就要重叠大面，得到5×8×6的长方体，这个长方体的表面积为

  ；
  在图2的基础上继续摆，要使表面积小，就要重叠大面，得到10×4×6的长方体，这个长方体的表面积为

  ；
  在图3的基础上继续摆，要使表面积小，就要重叠大面，得到5×8×6的长方体，这个长方体的表面积为

  ；
  综上所述，有4个相同的长方体纸盒，它们的长、宽、高分别是5、4、3，要用这4个纸盒搭成一个大长方体的表面积最小为

  ．
  探究三：我们知道，在体积相同的前提下，正方体的表面积最小，所以我们可以尽可能地使所搭成的几何体为正方体或接近正方体，我们还可以这样思考：
  将4分解质因数，得到1×1×4，或1×2×2两种情况，通过与小长方体的长宽高5×4×3进行组合：
  在L=5×1=5，K=4×2=8，H=3×2=6时，搭成的L×K×H的大长方体最接近正方体，此时表面积最小，表面积为2（L×K+K×H+L×H）=

  （直接写出结果）．
  类比应用：请你仿照探究三的解题思路，解答开始提出的问题：
  有12个相同的长方体纸盒，它们的长、宽、高分别是4、3、5，现要用这12个纸盒搭成一个大长方体，怎样搭可使长方体的表面积最小？
  拓展延伸：将168个棱长为1cm的小正方体，拼成一个长方体，使得长方体的表面积达到最小，这个表面积是

  cm²．
  组卷：374引用：3难度：0.5

  解析

• 24．如图，四边形ABCD中，AD∥BC，∠ADC=90°，AD=CD=8，BC=6，点M从点D出发，以每秒2个单位长度
  的速度向点A运动，同时，点N从点B出发，以每秒1个单位长度的速度向点C运动．当其中一个动点到达终点时，另一个动点也随之停止运动．过点N作NP⊥AD于点P，连接AC交MP于点Q，连接MQ，设运动时间为t秒（0＜t＜4）．
  （1）连接AN，CP，当t为何值时，四边形ANCP为平行四边形；
  （2）在运动过程中，是否存在某一时刻t,使得CM平分∠ACD，若存在，求出t的值；若不存在，请说明理由．
  （3）设四边形DMQC的面积为y,求y与t的函数关系式；
  （4）将△AQM沿AD翻折，得到△AKM在运动过程中，是否存在某时刻t,使四边形AQMK为菱形，若存在，求出t的值；若不存在，请说明理由．
  
  组卷：273引用：2难度：0.1

  解析