2023-2024学年北京五十七中八年级（上）期中数学试卷

一、选择题（本题共30分，每小题3分）

• 1．下列图形中，不是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：618引用：119难度：0.7

  解析

• 2．一个多边形的内角和是外角和的3倍，则这个多边形是（　　）

  A．六边形

  B．七边形

  C．八边形

  D．九边形
  组卷：1063引用：29难度：0.9

  解析

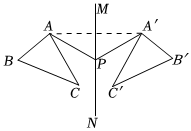• 3．如图，△ABC与△A'B'C'关于直线MN对称，P为MN上任一点，下列结论中错误的是（　　）

  A．△AA′P是等腰三角形

  B．MN垂直平分CC'

  C．△ABC与△A'B'C'周长相等

  D．直线AB、A'B'的交点不一定在MN上
  组卷：81引用：4难度：0.6

  解析

• 4．如图，AC与BD相交于点O，AB=DC，要使△ABO≌△DCO，则需添加的一个条件可以是（　　）

  A．OB=OC

  B．∠A=∠D

  C．OA=OD

  D．∠AOB=∠DOC
  组卷：893引用：17难度：0.5

  解析

• 5．如图，在△ABC中，AB=AC，D为BC上一点，且DA=DC，BD=BA，则∠B的大小为（　　）

  A．40°

  B．36°

  C．30°

  D．25°
  组卷：7456引用：62难度：0.7

  解析

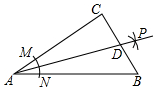• 6．如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交边AC、AB于点M、N，再分别以点M、N为圆心，大于MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=4，AB=15，则△ABD的面积是（　　）

  A．120

  B．60

  C．45

  D．30
  组卷：235引用：5难度：0.6

  解析

• 7．如图，在△ABC中，∠A=60°，∠ABC=50°，∠B、∠C的平分线相交于F，过点F作DE∥BC，交AB于D，交AC于E，那么下列结论正确的是（　　）
  ①∠ACB=70°；②∠BFC=115°；③∠BDF=130°；④∠CFE=40°．

  A．①②

  B．③④

  C．①③

  D．①②③
  组卷：260引用：7难度：0.9

  解析

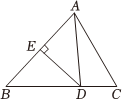• 8．如图，在△ABC中，DE垂直平分AB．若AD=4，BC=3CD，则BC的长为（　　）

  A．3

  B．4

  C．5

  D．6
  组卷：281引用：3难度：0.5

  解析

三、解答题（本题共46分）

• 25．如图，Rt△ACB中，∠ACB=90°，AC=BC，E点为射线CB上一动点，连接AE，作AF⊥AE且AF=AE．
  （1）如图1，过F点作FD⊥AC交AC于D点，求证：△ADF≌△ECA，并写出EC、CD和DF的数量关系；
  （2）如图2，连接BF交AC于G点，若

  AG

  CG

  =

  3

  ，求证：E点为BC中点；
  （3）当E点在射线CB上，连接BF与直线AC交于G点，若

  BC

  BE

  =

  7

  3

  ，求

  AG

  CG

  ．
  
  组卷：708引用：3难度：0.1

  解析

• 26．在平面直角坐标系xOy中，将点M（x,y）到x轴和y轴的距离的较大值定义为点M的“相对轴距”，记为d（M）．即：如果|x|≥|y|，那么d（M）=|x|；如果|x|＜|y|，那么d（M）=|y|．例如：点M（1，2）的“相对轴距”d（M）=2．
  （1）点P（-2，1）的“相对轴距”d（P）=

  ；
  （2）请在图1中画出“相对轴距”与点P（-2，1）的“相对轴距”相等的点组成的图形；
  （3）已知点A（1，1），B（2，3），C（3，2），点M，N是△ABC内部（含边界）的任意两点．
  ①直接写出点M与点N的“相对轴距”之比

  d

  （

  M

  ）

  d

  （

  N

  ）

  的取值范围；
  ②将△ABC向左平移k（k＞0）个单位得到△A'B'C'，点M'与点N'为△A'B'C'内部（含边界）的任意两点，并且点M'与点N'的“相对轴距”之比

  d

  （

  M

  ′

  ）

  d

  （

  N

  ′

  ）

  的取值范围和点M与点N的“相对轴距”之比

  d

  （

  M

  ）

  d

  （

  N

  ）

  的取值范围相同，请直接写出k的取值范围．
  
  组卷：1271引用：5难度：0.6

  解析