2023-2024学年浙江省杭州市萧山区八年级（上）期中数学试卷

一、选择题（共10小题，每小题3分，共30分）

• 1．如图所示图形中，为轴对称的图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：9引用：1难度：0.9

  解析

• 2．已知三角形的三边长分别为4，5，x,则x不可能是（　　）

  A．3

  B．5

  C．7

  D．9
  组卷：855引用：89难度：0.9

  解析

• 3．在△ABC中，画出边AC上的高，画法正确的是（　　）

  A．

  B．

  C．

  D．
  组卷：4219引用：39难度：0.9

  解析

• 4．对于命题“如果∠1与∠2互补，那么∠1=∠2=90°”，能说明这个命题是假命题的反例是（　　）

  A．∠1=80°，∠2=110°	B．∠1=10°，∠2=169°
  C．∠1=60°，∠2=120°	D．∠1=60°，∠2=140°
  组卷：408引用：8难度：0.7

  解析

• 5．在△ABC中，线段AP，AQ，AR分别是BC边上的高线，中线和角平分线，则（　　）

  A．AP≤AQ

  B．AQ≤AR

  C．AP＞AR

  D．AP＞AQ
  组卷：1078引用：9难度：0.8

  解析

• 6．根据下列已知条件，能画出唯一的△ABC的是（　　）

  A．AB=3，BC=4，AC=7	B．AB=4，BC=3，∠A=30°
  C．∠A=60°，∠B=45°，AC=4	D．∠A=∠B，AB=6
  组卷：203引用：5难度：0.7

  解析

• 7．如图，△ABC中，D为AB中点，E在AC上，且BE⊥AC．若DE=5，AE=8，EC=

  7

  ，则BC的长度是（　　）

  A． 29

  B．8

  C． 43

  D． 71
  组卷：149引用：2难度：0.6

  解析

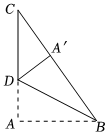• 8．如图，Rt△ABC中，∠A=90°，AB=3，AC=4，现将△ABC沿BD进行翻折，使点A刚好落在BC上，则CD的长为（　　）

  A． 5 2

  B． 2 5

  C．2

  D． 3 2
  组卷：796引用：10难度：0.7

  解析

三、解答题（共8小题，66分，解答应写出文字说明或推理步骤）

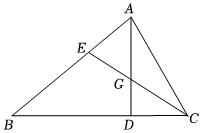• 23．如图，在锐角△ABC中，点E是AB边上一点，BE=CE，AD⊥BC于点D，AD与EC交于点G．
  （1）求证：△AEG是等腰三角形．
  （2）若BE=10，CD=3，G为CE中点，求AG的长．
  组卷：405引用：3难度：0.5

  解析

• 24．如图，在Rt△ABC中，∠ABC=90°，AB=4，BC=3，点D为AC边上的动点，点D从点C出发，沿边CA往A运动，当运动到点A时停止，若设点D运动的时间为t秒，点D运动的速度为每秒1个单位长度．
  （1）当t=2时，分别求CD和AD的长；
  （2）当t为何值时，△CBD是直角三角形？
  （3）若△CBD是等腰三角形，请直接写出t的值．
  组卷：907引用：5难度：0.1

  解析