2021-2022学年福建省龙岩七中八年级（上）第一次月考数学试卷

一.选择题​

• 1．下列每组数分别是三根小木棒的长度，用它们能摆成三角形的是（　　）

  A．3cm,4cm,8cm	B．8cm,7cm,15cm
  C．5cm,5cm,11cm	D．12cm,12cm,20cm
  组卷：5396引用：110难度：0.9

  解析

• 2．如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（　　）

  A．

  B．

  C．

  D．
  组卷：19830引用：261难度：0.9

  解析

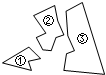• 3．如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（　　）

  A．带①去

  B．带②去

  C．带③去

  D．带①和②去
  组卷：7466引用：575难度：0.7

  解析

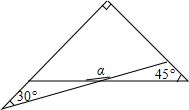• 4．一副三角板有两个直角三角形，如图叠放在一起，则∠α的度数是（　　）

  A．165°

  B．120°

  C．150°

  D．135°
  组卷：1755引用：91难度：0.9

  解析

• 5．如果三角形的三个内角的度数比是2：3：4，则它是（　　）

  A．锐角三角形	B．钝角三角形
  C．直角三角形	D．钝角或直角三角形
  组卷：6684引用：73难度：0.9

  解析

• 6．一个等腰三角形的两边长分别为3和5，则它的周长为（　　）

  A．7

  B．9

  C．11或13

  D．9 或12
  组卷：161引用：2难度：0.6

  解析

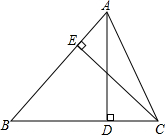• 7．如图，AD，CE是△ABC的两条高，已知AD=10，CE=9，AB=12，则BC的长是（　　）

  A．10

  B．10.8

  C．12

  D．15
  组卷：485引用：9难度：0.9

  解析

• 8．如图，已知∠ABC=∠DCB，下列所给条件不能证明△ABC≌△DCB的是（　　）

  A．∠A=∠D

  B．AB=DC

  C．∠ACB=∠DBC

  D．AC=BD
  组卷：6346引用：147难度：0.9

  解析

​三、解答题

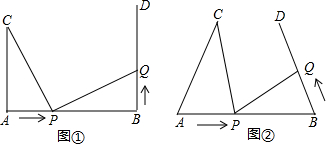• 24．如图①，AB=6cm,AC⊥AB，BD⊥AB，AC=BD=4cm,点P在线段AB上以2cm/s的速度由点A向点B运动，同时点Q在线段BD上由点B向点D运动，它们的运动时间为t s.
  （1）当点P、Q的运动速度相同且t=1时，求证：△ACP≌△BPQ；
  （2）将图①中的“AC⊥AB，BD⊥AB”，改为“∠CAB=∠DBA=70°”，其他条件不变，得到图②．设点Q的运动速度为v cm/s,若△ACP和以B、P、Q为顶点的三角形全等，求v的值．
  组卷：112引用：2难度：0.5

  解析

• 25．【初步探索】
  （1）如图1，AD是△ABC的中线，探究AB+AC与2AD的大小关系．
  小明同学探究此问题的方法是：延长AD至点E，使DE=AD，连接BE，先证明△ADC≌△EDB，可得出结论，他的结论应是

  
  【灵活运用】
  （2）如图2，AD是△ABC的中线，E、F分别在AB、AC上，且DE⊥DF，求证：BE+CF＞EF．
  【拓展延伸】
  （3）如图3，AD为△ABC的角平分线，直线MN⊥AD于点A．点E为MN上一点（与点A不重合），△ABC周长记为a,△EBC周长记为b,比较a与b的数量关系并证明．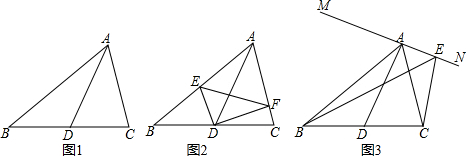
  
  组卷：848引用：2难度：0.3

  解析