2023-2024学年黑龙江省哈尔滨四十九中八年级（上）月考数学试卷（9月份）（五四学制）

一、单选题（每题3分，共计30）

• 1．2022年暑假期间，国家高度重视预防溺水安全工作，要求各级各类学校积极落实防溺水安全教育．以下与防溺水相关的标志中是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：59引用：10难度：0.9

  解析

• 2．在平面直角坐标系中，点（2，-1）关于x轴对称的点是（　　）

  A．（2，1）

  B．（1，-2）

  C．（-1，2）

  D．（-2，-1）
  组卷：730引用：28难度：0.9

  解析

• 3．已知等腰三角形的一边等于3，一边等于6，则它的周长为（　　）

  A．12

  B．12或15

  C．15

  D．15或18
  组卷：350引用：14难度：0.9

  解析

• 4．明明家有一块三角形菜地，现要在该菜地种一棵柿子树，使得柿子树到菜地三个顶点的距离相等，则柿子树应种在菜地（　　）

  A．三条边的垂直平分线的交点处

  B．三个角的角平分线的交点处

  C．三条高的交点处

  D．三条中线的交点处
  组卷：49引用：6难度：0.7

  解析

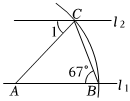• 5．如图，直线l₁∥l₂，以直线l₁上的点A为圆心、适当长为半径画弧，分别交直线l₁、l₂于点B、C，连接AC、BC．若∠ABC=67°，则∠1=（　　）

  A．23°

  B．46°

  C．67°

  D．78°
  组卷：5423引用：61难度：0.9

  解析

• 6．在下列说法中，正确的是（　　）

  A．如果两个三角形全等，则它们一定能关于某直线成轴对称

  B．如果两个三角形关于某直线成轴对称，那么它们是全等三角形

  C．等腰三角形是以底边高线为对称轴的轴对称图形

  D．若两个图形关于某直线对称，则它们的对应点一定位于对称轴的两侧
  组卷：251引用：4难度：0.9

  解析

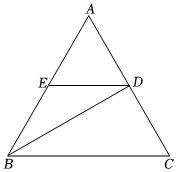• 7．如图，△ABC中，AB=AC，BC=BD，AD=DE=EB，则∠A的度数为（　　）

  A．55°

  B．45°

  C．36°

  D．30°
  组卷：38引用：9难度：0.7

  解析

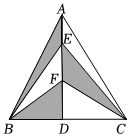• 8．如图，已知AD所在直线是△ABC的对称轴，点E、F是AD上的两点，若△ABC的面积为18．则图中阴影部分的面积是（　　）

  A．6

  B．12

  C．9

  D．无法确定
  组卷：155引用：5难度：0.6

  解析

三、解答题（其中19-20题各8分，21-25题各10分，共计66分）

• 24．小聪和小明两位同学在学习全等三角形时积极思考，提出了以下两个问题：
  问题1：如图1，△ABC中，AB=3，AC=2，AD是△ABC的角平分线，求BD：DC的值．
  小聪同学经过思考，发现可以过D作DM⊥AB于M，DN⊥AC于N，利用△ABD与△ACD的面积比来解决这个问题．
  问题2：如图2，△ABC为等边三角形，点D为△ABC外一点，∠CDA=60°，连接DB，探究AD，CD，BD三者之间的数量关系．
  小明同学经过思考，发现可以在DA上截取DE=DC，构造等边三角形CDE，从而解决这个问题．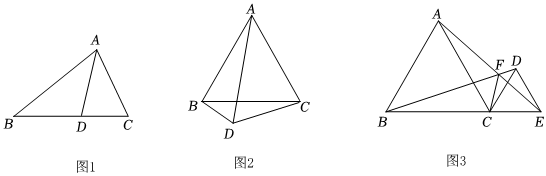
  
  （1）根据两位同学的思考，完成问题1、2的解答（直接写出结果）．
  （2）根据问题1、2的结论，解决下面问题：如图3，△ABC和△CDE都是等边三角形，且B、C、E三点共线，连接AE，BD交于点F，连接FC，设AF=a,DF=b,CF=c,若BC=2CE，直接写出

  a

  -

  2

  b

  3

  c

  的值．
  组卷：485引用：4难度：0.4

  解析

• 25．（1）如图1，在平面直角坐标系中，点O为坐标原点，点C的坐标为（0，6），在x轴的负半轴取点A，在x轴的正半轴取点B，△ABC面积等于36，AC=BC．求点A的坐标．
  （2）如图2，动点P以每秒2个单位长度的速度从点A出发沿AO方向向终点O运动，运动时间为t,过点P作DP⊥OA交AC于点D，在CB的延长线上取点E，使得AD=BE，连接DE交x轴于点G，若△DPG的面积为S，求S与t的关系式．
  （3）如图3，在（2）的条件下，以DE为底边，在x轴的上方作等腰直角三角形，使得DF=FE，∠F=90°，CE交DF于点K，DF交y轴于点Q，连接GQ，若GQ⊥DF，求点K坐标．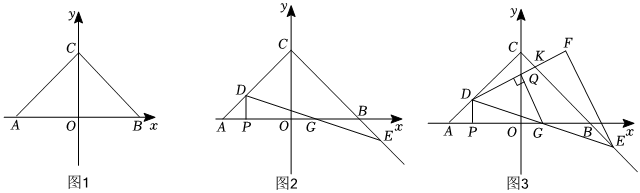
  组卷：66引用：1难度：0.2

  解析