当前位置：试卷中心 > 试卷详情

2023-2024学年江苏省徐州市铜山区黄集中心中学九年级（上）第一次学情调研数学试卷

发布：2024/9/22 1:0:8

一、单选题（每题3分，共36分）

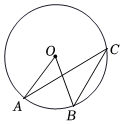1．如图，点A、B、C在⊙O上，∠ACB=30°，则∠AOB的度数是（　　）
A．30° B．40° C．60° D．65°
组卷：871引用：15难度：0.5
解析
2．用配方法将方程x²+6x-11=0变形，正确的是（　　）
A．（x-3）²=20 B．（x-3）²=2 C．（x+3）²=2 D．（x+3）²=20
组卷：150引用：14难度：0.9
解析
3．已知关于x的方程x²-4x+c+1=0有两个相等的实数根，则常数c的值为（　　）
A．-1 B．0 C．1 D．3
组卷：517引用：14难度：0.7
解析
4．已知圆锥的底面半径为3cm,母线长为5cm,则圆锥的侧面积是（　　）
A．15πcm² B．15cm² C．20πcm² D．20cm²
组卷：1117引用：24难度：0.9
解析
5．已知扇形半径为6，弧长为4π，则扇形面积为（　　）
A．10π B．12π C．16π D．24π
组卷：531引用：4难度：0.9
解析
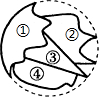6．小明不慎把家里的圆形镜子打碎了，其中四块碎片如图所示，为了配到与原来大小一样的圆形镜子，小明带到商店去的一块碎片应该是（　　）
A．第一块 B．第二块 C．第三块 D．第四块
组卷：2746引用：13难度：0.7
解析
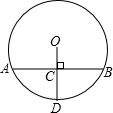7．如图，已知半径OD与弦AB互相垂直，垂足为点C，若AB=8cm,CD=3cm,则圆O的半径为（　　）
A．
25
6
cm B．5cm C．4cm D．
19
6
cm
组卷：687引用：68难度：0.9
解析
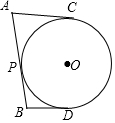8．如图，AB、AC、BD是⊙O的切线，切点分别为P、C、D．若AB=5，BD=2，则AC的长是（　　）
A．2.5 B．3 C．3.5 D．2
组卷：267引用：3难度：0.7
解析
9．在平面直角坐标系xOy中，点M的坐标为（2，0），⊙M的半径为4，则点P（-2，3）与⊙M的位置关系是（　　）
A．点P在⊙M内 B．点P在⊙M上 C．点P在⊙M外 D．不能确定
组卷：111引用：2难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题

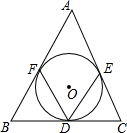26．如图，⊙O是△ABC的内切圆，切点分别为D、E、F，∠B=60°，∠C=70°，求∠EDF的度数．
组卷：293引用：3难度：0.5
解析
27．【问题背景】
如图1，在四边形ADBC中，∠ACB=∠ADB=90°，AD=BD，探究线段AC，BC，CD之间的数量关系．
小吴同学探究此问题的思路是：将△BCD绕点D，逆时针旋转90°到△AED处，点B，C分别落在点A，E处（如图2），易证点C，A，E在同一条直线上，并且△CDE是等腰直角三角形，所以CE=
2
CD，从而得出结论：AC+BC=
2
CD
【简单应用】
（1）在图1中，若AC=
2
，BC=2
2
，则CD=
．
（2）如图3，AB是⊙O的直径，点C、D在⊙O上，
ˆ
AD
=
ˆ
BD
，若AB=13，BC=12，求CD的长．
【拓展规律】
（3）如图4，∠ACB=∠ADB=90°，AD=BD，若AC=m,BC=n（m＜n），求CD的长（用含m,n的代数式表示）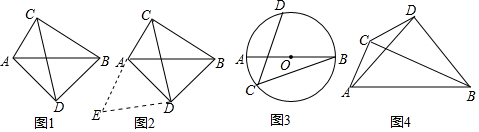
组卷：622引用：15难度：0.1
解析