2022-2023学年福建省泉州外国语中学高二(上)期中数学试卷
发布:2024/9/14 2:0:8
一、单项选择题(每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1.直线3x+3y+1=0的倾斜角是( )
组卷:234引用:44难度:0.9 -
2.若直线2x+(a+2)y+4=0与直线(a-1)x+2y+2=0平行,则实数a的值为( )
组卷:286引用:6难度:0.8 -
3.三棱柱ABC-A1B1C1中,N是A1B的中点,若
=CA,a=CB,b=CC1,则c=( )CN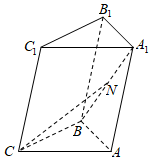 组卷:498引用:8难度:0.7
组卷:498引用:8难度:0.7 -
4.若直线mx+ny+3=0在y轴上的截距为-1,且它的倾斜角是直线x-2y=3的倾斜角的2倍,则( )
组卷:55引用:3难度:0.7 -
 5.如图,在棱长为1的正方体ABCD-A1B1C1D1中,M是AA1的中点,则点A1到平面MBD的距离是( )组卷:103引用:5难度:0.6
5.如图,在棱长为1的正方体ABCD-A1B1C1D1中,M是AA1的中点,则点A1到平面MBD的距离是( )组卷:103引用:5难度:0.6 -
6.直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与NA所成的角的余弦值为( )
组卷:101引用:3难度:0.5 -
7.两圆x2+y2+2ax+a2-4=0和x2+y2-4by-1+4b2=0恰有三条公切线,若a∈R,b∈R,且ab≠0,则
的最小值为( )1a2+1b2组卷:245引用:31难度:0.7
四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
-
 21.如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体.
21.如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体.
(Ⅰ)求证:AB⊥平面ADC;
(Ⅱ)若AD=1,二面角C-AB-D的平面角的正切值为,求二面角B-AD-E的余弦值.6组卷:521引用:12难度:0.5 -
22.某公园有一形状可抽象为圆柱的标志性景观建筑物.该建筑物底面直径为8米,在其南面有一条东西走向的观景直道,建筑物的东西两侧有与观景直道平行的两段辅道,观景直道与辅道距离10米.在建筑物底面中心O的东北方向20
米的点A处,有一360°全景摄像头,其安装高度低于建筑物的高度.2
(1)在西辅道上距离建筑物1米处的游客,是否在该摄像头的监控范围内?
(2)求观景直道不在该摄像头的监控范围内的长度.组卷:50引用:4难度:0.5


