当前位置：试卷中心 > 试卷详情

2023-2024学年江西省宜春市宜丰中学创新部高二（上）第一次月考数学试卷（10月份）

发布：2024/9/11 14:0:9

一、单选题（40分）

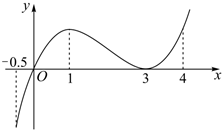1．设函数f（x）的导函数为f'（x），y=f'（x）的部分图象如图所示，则（　　）
A．函数f（x）在
（
-
1
2
，
1
）
上单调递增
B．函数f（x）在（0，4）上单调递增
C．函数f（x）在x=3处取得极小值
D．函数f（x）在x=0处取得极大值
组卷：200引用：6难度：0.6
解析
2．若
f
（
x
）
=
x
2
2
+
3
xf
′
（
3
）
，则曲线f（x）在x=3处的切线方程为（　　）
A．3x+2y+9=0 B．3x+2y-9=0 C．3x-2y+9=0 D．3x-2y-9=0
组卷：169引用：5难度：0.6
解析
3．在等比数列{a_n}中，a₁₀₁₂=2，若函数f（x）=
1
2
x
（
x
-
a
1
）
（
x
-
a
2
）
…
（
x
-
a
2023
）
，则f'（0）=（　　）
A．-2²⁰²² B．2²⁰²² C．-2²⁰²³ D．2²⁰²³
组卷：79引用：4难度：0.6
解析
4．函数f（x）=3x²-e^|x|的部分图象大致为（　　）
A． B． C． D．
组卷：104引用：8难度：0.5
解析
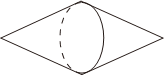5．如图，某几何体由两个相同的圆锥组成，且这两个圆锥有一个共同的底面，若该几何体的表面积为12π，体积为V，则V²的最大值为（　　）
A．
64
3
3
π
2
B．20
3
π
2
C．56
3
π
2
D．24
3
π
2
组卷：16引用：6难度：0.6
解析
6．若函数f（x）为定义在R上的偶函数，当x∈（-∞，0）时，f′（x）＞2x,则不等式f（3x-1）-f（2）＞（3x-3）（3x+1）的解集为（　　）
A．（-∞，-
1
3
） B．（-∞，-
1
3
）∪（1，+∞）
C．（1，+∞） D．（-
1
3
，1）
组卷：336引用：6难度：0.6
解析
7．已知函数
f
（
x
）
=
ax
e
x
+
lnx
-
x
有唯一的极值点t,则f（t）的取值范围是（　　）
A．[-2，+∞） B．[-3，+∞） C．[2，+∞） D．[3，+∞）
组卷：482引用：16难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（70分）

21．已知函数f（x）=-ax²+xlnx+2．
（l）若f（x）有两个极值点，求实数a的取值范围；
（2）当a=0时，证明：f（x）＞x-
2
x
．
组卷：98引用：7难度：0.4
解析
22．已知函数f（x）=lnx,g（x）=ax²+bx（a≠0，b∈R）．
（1）若a=2，b=3，求函数F（x）=f（x）-g（x）的单调区间；
（2）若函数f（x）与g（x）的图象有两个不同的交点（x₁，f（x₁）），（x₂，f（x₂）），记
x
0
=
x
1
+
x
2
2
，记f'（x），g'（x）分别是f（x），g（x）的导函数，证明：f'（x₀）＜g'（x₀）．
组卷：67引用：2难度：0.5
解析