2023-2024学年四川省南充市阆中市东风中学高二（上）第一次段考数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分.

• 1．若向量

  a

  =（2，-3，1）和

  b

  =（1，x,4）满足条件

  a

  •

  b

  =0，则x的值是（　　）

  A．-1

  B．0

  C．1

  D．2
  组卷：790引用：3难度：0.8

  解析

• 2．直线

  3

  3

  x

  +

  y

  -

  7

  =

  0

  的倾斜角是（　　）

  A． π 6

  B． - π 6

  C． 2 π 3

  D． 5 π 6
  组卷：86引用：3难度：0.5

  解析

• 3．已知平面α的一个法向量是（2，-1，1），α∥β，则下列向量可作为平面β的一个法向量的是（　　）

  A．（4，2，-2）

  B．（2，0，4）

  C．（2，-1，-5）

  D．（4，-2，2）
  组卷：125引用：6难度：0.8

  解析

• 4．已知直线l₁：ax+2y+6=0，l₂：x+（a-1）y+3=0，若l₁∥l₂，则a=（　　）

  A．-1

  B．2

  C． 2 3

  D．2或-1
  组卷：101引用：10难度：0.8

  解析

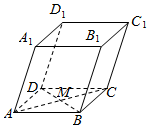• 5．如图，平行六面体ABCD-A₁B₁C₁D₁中，AC与BD的交点为M，设

  AB

  =

  a

  ，

  AD

  =

  b

  ，

  A

  A

  1

  =

  c

  ，则选项中与向量

  M

  C

  1

  相等的是（　　）

  A． - 1 2 a - 1 2 b - c

  B． 1 2 a + 1 2 b + c

  C． 1 2 a - 1 2 b - c

  D． 1 2 a + 1 2 b - c
  组卷：248引用：10难度：0.7

  解析

• 6．设l,m,n均为直线，其中m,n在平面α内，则“l⊥α”是“l⊥m且l⊥n”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：527引用：49难度：0.9

  解析

• 7．我们称：两个相交平面构成四个二面角，其中较小的二面角称为这两个相交平面的夹角；由正方体的四个顶点所确定的平面统称为该正方体的“表截面”．则在正方体中，两个不重合的“表截面”的夹角大小不可能为（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  组卷：104引用：4难度：0.6

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．如图，在四棱锥S-ABCD中，底面ABCD满足AB⊥AD，AB⊥BC，SA⊥底面ABCD，且SA=AB=BC=2，AD=1．
  （1）求三棱锥C-SBD的体积；
  （2）求平面SCD与平面SAB的夹角的余弦值．
  组卷：16引用：1难度：0.4

  解析

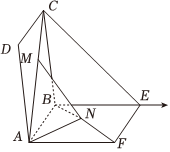• 22．在如图所示的试验装置中，两个正方形框架ABCD，ABEF的边长都是1，且它们所在的平面互相垂直．活动弹子M，N分别在正方形对角线AB，BF上移动，且CM，BN的长度保持相等，记

  CM

  =

  BN

  =

  a

  （

  0

  ＜

  a

  ＜

  2

  ）

  ．
  （1）求异面直线AC，BF所成角的余弦值；
  （2）a为何值时，MN的长最小？
  （3）当MN的长最小时，求AB与平面AMN夹角的余弦值．
  组卷：21引用：1难度：0.5

  解析