2022-2023学年重庆市铜梁区巴川中学八年级(下)期末数学试卷
发布:2024/6/8 8:0:9
一、选择题(本大题共10个小题每小题4分,共40分)在每个小题的下面,都给出了代号为A。B、C、D的四个答案,其中只有一个是正确的请将答题卡上对应题目的正确答案标号涂黑
-
1.下列二次根式中属于最简二次根式的是( )
组卷:335引用:3难度:0.8 -
2.以下列各组数为边长,能构成直角三角形的是( )
组卷:63引用:3难度:0.7 -
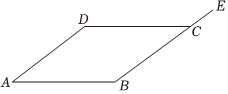 3.如图在平行四边形ABCD中,点E在线段BC的延长线上,若∠DCE=140°.则∠A的度数是( )组卷:23引用:1难度:0.5
3.如图在平行四边形ABCD中,点E在线段BC的延长线上,若∠DCE=140°.则∠A的度数是( )组卷:23引用:1难度:0.5 -
4.八年级的甲,乙,丙,丁四位同学进行跳绳练习,每人的10次跳绳练习的平均成绩均是180个/分钟,但四人的成绩方差分别是
,S2甲=0.15,S2乙=0.32,S2丙=0.5,成绩最稳定的同学是( )S2丁=0.25组卷:31引用:1难度:0.5 -
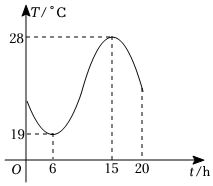 5.如图所示的是一台自动测温记录仪记录的图象,它反映了重庆5月某天一段时间的气温T(℃)随时间t变化的情况,观察图象得到的下列信息,其中错误的是( )组卷:278引用:3难度:0.7
5.如图所示的是一台自动测温记录仪记录的图象,它反映了重庆5月某天一段时间的气温T(℃)随时间t变化的情况,观察图象得到的下列信息,其中错误的是( )组卷:278引用:3难度:0.7 -
6.估计
的值应在( )(22+3)×2组卷:479引用:9难度:0.7 -
7.对于一次函数y=-3x+m,下列说法正确的是( )
组卷:473引用:3难度:0.7 -
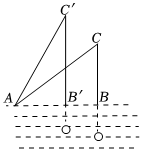 8.如图,露在水面上的鱼线BC长为3m.钓鱼者想看看鱼钩上的情况把鱼竿AC提起到AC′的位置,此时露在水面上的鱼线B'C′长为4m,若BB′的长为1m,试问的鱼竿AC有多长?设AB′长xm,则下所列方程正确的是( )组卷:458引用:6难度:0.5
8.如图,露在水面上的鱼线BC长为3m.钓鱼者想看看鱼钩上的情况把鱼竿AC提起到AC′的位置,此时露在水面上的鱼线B'C′长为4m,若BB′的长为1m,试问的鱼竿AC有多长?设AB′长xm,则下所列方程正确的是( )组卷:458引用:6难度:0.5
三、解答题(本大题共8个小题,其中19题8分,其余各小题每小题8分,共78分)解答题时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括作辅助线),请将解答过程书写在答题卡中对应的位置上.
-
25.如图1,在平面直角坐标系中,直线l1:y=-x+5与y轴交于点A,直线l2:y=kx+b与x轴、y轴分别交于点B(-4,0)和点C,直线l1与直线l2交于点D(2,d).
(1)求直线l2的解析式;
(2)若点E为线段BC上一个动点,过点E作EF⊥x轴于点F,交直线l1于点G,当EG+BF=时,求△EGD的面积;253
(3)如图2,将l2向右平移6个单位长度得到直线l3,直线l3与直线l1交于点H,点D关于y轴的对称点为点G,点M为直线l1上一个动点,点N为直线l2上一个动点.若以点G,H,M,N为顶点的四边形是平行四边形,直接写出所有满足条件的点M的坐标并写出求其中一个点M坐标的过程.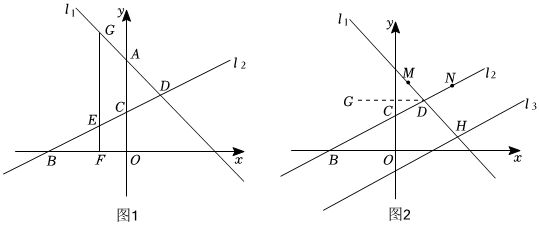 组卷:162引用:1难度:0.2
组卷:162引用:1难度:0.2 -
26.在正方形ABCD中,E为直线AB上一点.
(1)如图1,E在AB延长线上,F为对角线BD上一点,连接EF,AF,CF,若EF=CF,求∠EFC度数;
(2)如图2,E在AB边上,连接DE,点H在BC边上且BH=2AE,过点H作HQ⊥DE,垂足为Q,延长HQ交AD于点G,连接AQ.求证:;EQ+GQ=2AQ
(3)如图3,E在AB边上运动,连接DE,取DE中点M.点N在CD边上运动,连接BN,将△BCN沿着BN翻折到同一平面内得到△BC′N.当点M与点C′重合时,直接写出的值.CNAE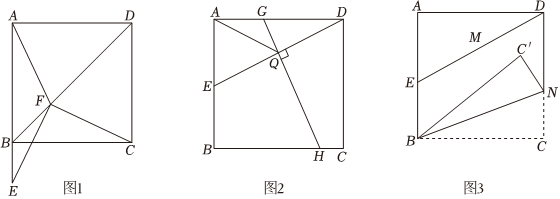 组卷:224引用:1难度:0.1
组卷:224引用:1难度:0.1


