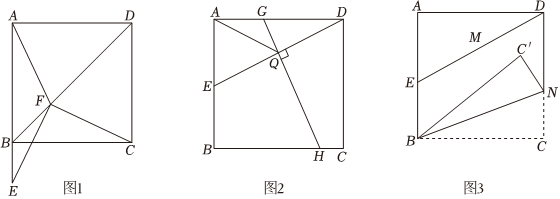
在正方形ABCD中，E为直线AB上一点．
（1）如图1，E在AB延长线上，F为对角线BD上一点，连接EF，AF，CF，若EF=CF，求∠EFC度数；
（2）如图2，E在AB边上，连接DE，点H在BC边上且BH=2AE，过点H作HQ⊥DE，垂足为Q，延长HQ交AD于点G，连接AQ．求证：EQ+GQ=2AQ；
（3）如图3，E在AB边上运动，连接DE，取DE中点M．点N在CD边上运动，连接BN，将△BCN沿着BN翻折到同一平面内得到△BC′N．当点M与点C′重合时，直接写出CNAE的值．
EQ
+
GQ
=
2
AQ
CN
AE
【考点】相似形综合题．
【答案】（1）90°；
（2）证明过程详见解答；
（3）．
（2）证明过程详见解答；
（3）
2
3
+
3
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/4 8:0:5组卷：225引用：1难度：0.1
相似题
-
1．如图1，在△ABC中，∠BCA=90°，AC=3，BC=4，点P为斜边AB上一点，过点P作射线PD⊥PE，分别交AC、BC于点D，E．
（1）问题产生
若P为AB中点，当PD⊥AC，PE⊥BC时，=；PDPE
（2）问题延伸
在（1）的情况下，将若∠DPE绕着点P旋转到图2的位置，的值是否会发生改变？如果不变，请证明；如果改变，请说明理由；PDPE
（3）问题解决
如图3，连接DE，若△PDE与△ABC相似，求BP的值．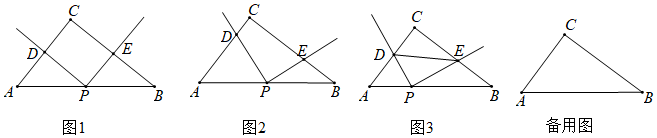
发布：2025/6/14 0:0:1组卷：966引用：6难度：0.1 -
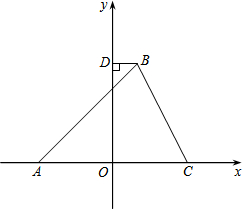2．如图，在平面直角坐标系中，△ABC的顶点A在x轴负半轴上，顶点C在x轴正半轴上，顶点B在第一象限，过点B作BD⊥y轴于点D，线段OA，OC的长是一元二次方程x2-12x+36=0的两根，BC=4，∠BAC=45°．5
（1）求点A，C的坐标；
（2）反比例函数y=的图象经过点B，求k的值；kx
（3）在y轴上是否存在点P，使以P，B，D为顶点的三角形与以P，O，A为顶点的三角形相似？若存在，请写出满足条件的点P的个数，并直接写出其中两个点P的坐标；若不存在，请说明理由．发布：2025/6/14 10:30:2组卷：1994引用：7难度：0.5 -
3．从三角形（不是等腰三角形）的一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中，一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．
（1）如图①，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线；
（2）在△ABC中，∠A=48°，CD是△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数；
（3）如图②，在△ABC中，AC=3，BC=，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长．3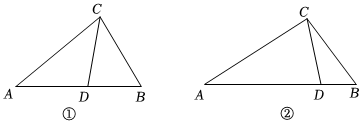
发布：2025/6/13 23:0:1组卷：439引用：2难度：0.2
