2022-2023学年广东省佛山市桂城街道七年级（下）调研数学试卷

一、选择题（本大题共10小题，每小题3分，共30分）

• 1．如所示四个图案中，不是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：34引用：1难度：0.9

  解析

• 2．下列运算中，正确的是（　　）

  A．-（m+n）=n-m	B．（m3n2）3=m6n5
  C．m3•m2=m5	D．n3÷n3=n
  组卷：372引用：12难度：0.9

  解析

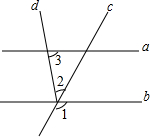• 3．如图，直线a∥b,∠1=120°，∠2=40°，则∠3等于（　　）

  A．60°

  B．70°

  C．80°

  D．90°
  组卷：699引用：82难度：0.9

  解析

• 4．袋中有红球4个，白球若干个，它们只有颜色上的区别．从袋中随机地取出一个球，如果取到白球的可能性较大，那么袋中白球的个数可能是（　　）

  A．3个	B．不足3个
  C．4个	D．5个或5个以上
  组卷：1834引用：74难度：0.9

  解析

• 5．已知（3x+a）²=9x²+bx+4，则b的值为（　　）

  A．6

  B．±6

  C．12

  D．±12
  组卷：1939引用：6难度：0.9

  解析

• 6．如图，在四边形ABCD中，AB=CD，BA和CD的延长线交于点E，若点P使得S_△PAB=S_△PCD，则满足此条件的点P（　　）#ZZ04

  A．有且只有1个

  B．有且只有2个

  C．组成∠E的角平分线

  D．组成∠E的角平分线所在的直线（点E除外）
  组卷：80引用：2难度：0.5

  解析

• 7．在2⁷⁷，3⁵⁵，5⁴⁴，6³³这四个数中，最大的数是（　　）

  A．277

  B．355

  C．544

  D．633
  组卷：970引用：7难度：0.9

  解析

五、解答题（三）（本大题共2小题，每小题12分，共24分）

• 22．【阅读材料】配方法是数学中重要的一种思想方法．它是指将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法．这种方法常被用到代数式的变形中，并结合非负数的意义来解决一些问题．
  我们定义：一个整数能表示成a²+b²（a、b是整数）的形式，则称这个数为“完美数”．例如，5是“完美数”．理由：因为5=2²+1²，所以5是“完美数”．
  【解决问题】
  （1）数61

  “完美数”（填“是”或“不是”）；
  【探究问题】
  （2）已知x²+2y²-4x+4y+6=0，则x+y=

  ；
  （3）已知S=5x²+y²+2xy+12x+k（x、y是整数，k是常数），要使S为“完美数”，试求出符合条件的k值，并说明理由．
  【拓展结论】
  （4）已知x、y满足-x²+

  2

  3

  x-y+1=0，求7x-3y的最小值．
  组卷：377引用：3难度：0.5

  解析

• 23．已知：如图①长方形纸片ABCD中，AB＜AD．将长方形纸片ABCD沿直线AE翻折，使点B落在AD边上，记作点F，如图②．
  
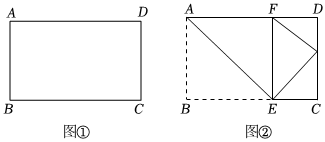
  （1）当AD=10，AB=6时，求线段FD的长度；
  （2）设AD=10、AB=x,如果再将△AEF沿直线EF向右翻折，使点A落在射线FD上，记作点G，若设线段FD=

  4

  3

  DG，请根据题意画出图形，并求出x的值；
  （3）设AD=a,AB=b,△AEF沿直线EF向右翻折后交CD边于点H，连接FH当

  S

  △

  HFE

  S

  四边形

  ABCD

  =

  1

  5

  时，求

  a

  b

  的值．
  组卷：74引用：2难度：0.4

  解析