当前位置：试卷中心 > 试卷详情

2022-2023学年四川省成都市金牛区协同外国语学校九年级（上）月考数学试卷（10月份）

发布：2024/8/17 18:0:1

一、选择题（每小题4分，共32分）

1．下列方程，是一元二次方程的是（　　）
A．2x+1=0 B．y²+x=1 C．x²+x-1=0 D．
1
x
+x²=1
组卷：150引用：9难度：0.9
解析
2．已知关于x的一元二次方程x²-kx-4=0的一个根为2，则另一根是（　　）
A．4 B．1 C．2 D．-2
组卷：258引用：44难度：0.9
解析
3．正方形具有而矩形不一定具有的性质是（　　）
A．四个角都是直角 B．对角线相等
C．对角线互相垂直 D．对角线互相平分
组卷：1023引用：19难度：0.9
解析
4．如图，菱形OABC在平面直角坐标系中的位置如图所示，∠AOC=45°，OA=
2
，则点C的坐标为（　　）
A．（
2
，1） B．（1，1） C．（1，
2
） D．（
2
+1，1）
组卷：311引用：9难度：0.6
解析
5．已知三角形两边长分别为2和9，第三边的长为二次方程x²-14x+48=0的根，则这个三角形的周长为（　　）
A．11 B．17 C．17或19 D．19
组卷：1201引用：107难度：0.9
解析
6．如图，菱形ABCD中，对角线AC，BD相交于点O，点M是DC的中点．若菱形ABCD的周长为24，则OM的长为（　　）
A．12 B．8 C．6 D．3
组卷：301引用：6难度：0.5
解析
7．经过某十字路口的行人，可能直行，也可能左拐或右拐．假设这三种可能性相同，现有两人经过该路口，则恰有一人直行，另一人左拐的概率为（　　）
A．
1
9
B．
2
9
C．
1
3
D．
2
3
组卷：95引用：3难度：0.8
解析
8．已知方程ax²+bx+c=0的解是x₁=2，x₂=-3，则方程a（x+1）²+b（x+1）+c=0的解是（　　）
A．x₁=1，x₂=-4 B．x₁=-1，x₂=-4
C．x₁=-1，x₂=4 D．x₁=1，x₂=4
组卷：569引用：5难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

二、解答题（共30分）

25．如图，平面直角坐标系中，直线l分别交x轴、y轴于A、B两点（OA＜OB）且OA、OB的长分别是一元二次方程x²-（
3
+1）x+
3
=0的两个根，点C在x轴负半轴上，且AB：AC=1：2
（1）求A、C两点的坐标；
（2）若点M从C点出发，以每秒1个单位的速度沿射线CB运动，连接AM，设△ABM的面积为S，点M的运动时间为t,写出S关于t的函数关系式，并写出自变量的取值范围；
（3）点P是y轴上的点，在坐标平面内是否存在点Q，使以 A、B、P、Q为顶点的四边形是菱形？若存在，请直接写出Q点的坐标；若不存在，请说明理由．
组卷：3082引用：60难度：0.5
解析
26．已知正方形ABCD，E，F为平面内两点．

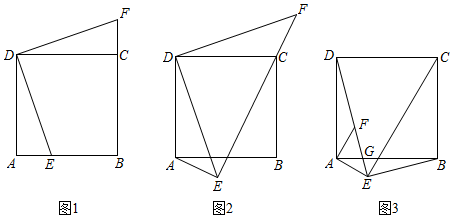
【探究建模】
（1）如图1，当点E在边AB上时，DE⊥DF，且B，C，F三点共线．求证：AE=CF；
【类比应用】
（2）如图2，当点E在正方形ABCD外部时，DE⊥DF，AE⊥EF，且E，C，F三点共线．猜想并证明线段AE，CE，DE之间的数量关系；
【拓展迁移】
（3）如图3，当点E在正方形ABCD外部时，AE⊥EC，AE⊥AF，DE⊥BE，且D，F，E三点共线，DE与AB交于G点．若DF=3，AE=
2
，求CE的长．
组卷：2497引用：17难度：0.1
解析