2022-2023学年浙江省金华市金东区海亮外国语学校八年级(上)月考数学试卷(12月份)
发布:2024/8/20 14:0:1
一、选择题(本题有10个小题,每小题3分,共30分)
-
1.下列图案不是轴对称图形的是( )
组卷:48引用:5难度:0.9 -
2.下列长度的三条线段能首尾相接构成三角形的是( )
组卷:1486引用:27难度:0.8 -
3.在平面直角坐标系中,点(4,3)关于x轴对称的点的坐标为( )
组卷:30引用:4难度:0.8 -
4.不等式x>5的解集在数轴上表示正确的是( )
组卷:728引用:4难度:0.9 -
5.在下列四个命题中,是真命题的是( )
组卷:74引用:3难度:0.5 -
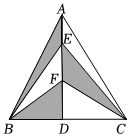 6.如图,已知AD所在直线是△ABC的对称轴,点E、F是AD上的两点,若△ABC的面积为18.则图中阴影部分的面积是( )组卷:157引用:5难度:0.6
6.如图,已知AD所在直线是△ABC的对称轴,点E、F是AD上的两点,若△ABC的面积为18.则图中阴影部分的面积是( )组卷:157引用:5难度:0.6 -
7.已知图中的两个三角形全等,则∠α等于( )
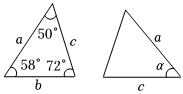 组卷:2762引用:59难度:0.7
组卷:2762引用:59难度:0.7 -
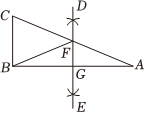 8.如图,在Rt△ABC中,∠ABC=90°,分别以点A和点B为圆心,大于的长为半径作弧相交于点D和点E,直线DE交AC于点F,交AB于点G,连接BF,若BC=2,AB=6,则△BCF的周长为( )12AB组卷:90引用:4难度:0.7
8.如图,在Rt△ABC中,∠ABC=90°,分别以点A和点B为圆心,大于的长为半径作弧相交于点D和点E,直线DE交AC于点F,交AB于点G,连接BF,若BC=2,AB=6,则△BCF的周长为( )12AB组卷:90引用:4难度:0.7
三、解答题(共66分)
-
 24.如图,△ABC是边长是12cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
24.如图,△ABC是边长是12cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
(1)当点Q到达点C时,PQ与AB的位置关系如何?请说明理由.
(2)在点P与点Q的运动过程中,△BPQ是否能成为等边三角形?若能,请求出t,若不能,请说明理由.
(3)则当t为何值时,△BPQ是直角三角形?组卷:247引用:12难度:0.4 -
25.通过对下面数学模型的研究学习,解决下列问题:
【模型呈现】
(1)如图1,∠BAD=90°,AB=AD,过点B作BC⊥AC于点C,过点D作DE⊥AC于点E.由∠1+∠2=∠2+∠D=90°,得∠1=∠D.又∠ACB=∠AED=90°,可以推理得到△ABC≌△DAE.进而得到AC=,BC=.我们把这个数学模型称为“K字”模型或“一线三等角”模型;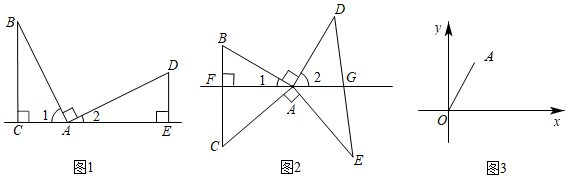
【模型应用】
(2)①如图2,∠BAD=∠CAE=90°,AB=AD,AC=AE,连接BC,DE,且BC⊥AF于点F,DE与直线AF交于点G.求证:点G是DE的中点;
②如图3,在平面直角坐标系xOy中,点A的坐标为(2,4),点B为平面内任一点.若△AOB是以OA为斜边的等腰直角三角形,请直接写出点B的坐标.组卷:3287引用:10难度:0.3


