2022-2023学年四川省宜宾市高二（下）期末数学试卷（理科）

一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合要求。

• 1．已知i为虚数单位，若复数z满足（1-i）z=1+i,则|z|=（　　）

  A．1

  B． 2

  C． 3

  D．2
  组卷：19引用：3难度：0.9

  解析

• 2．已知命题

  p

  ：

  ∀

  x

  ∈

  （

  0

  ，

  π

  ）

  ，

  sinx

  +

  1

  sinx

  ＞

  2

  ，则命题￢p为（　　）

  A． ∃ x 0 ∈ （ 0 ， π ） ， sin x 0 + 1 sin x 0 ＞ 2

  B． ∃ x 0 ∈ （ 0 ， π ） ， sin x 0 + 1 sin x 0 ≤ 2

  C． ∀ x ∈ （ 0 ， π ） ， sinx + 1 sinx ＜ 2

  D． ∀ x ∈ （ 0 ， π ） ， sinx + 1 sinx ≤ 2
  组卷：66引用：4难度：0.8

  解析

• 3．下列求导运算正确的是（　　）

  A． （ 1 x 2 ） ′ = 2 x 3	B． （ x ） ′ = 1 x
  C． （ x e x ） ′ = 1 - x e x	D．（cos（ex））′=esin（ex）
  组卷：147引用：2难度：0.8

  解析

• 4．如图是我国2012-2018年眼镜及其零件出口金额柱状图及同比增速折线图，则下列说法正确的是（　　）
  

  A．2012年至2018年我国眼镜及其零件出口金额逐年增加

  B．2012年至2018年我国眼镜及其零件出口金额的极差为16.41

  C．2013年至2018年我国眼镜及其零件出口金额同比增速逐年减少

  D．2013年至2018年我国眼镜及其零件出口金额同比增速最大的是2013年
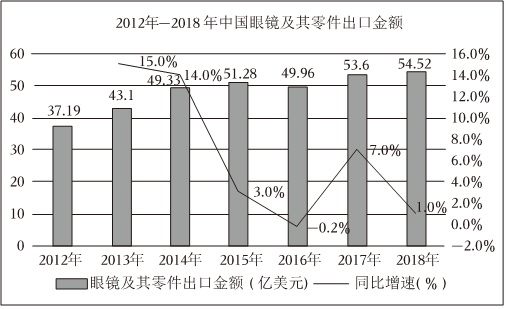  组卷：15引用：3难度：0.7

  解析

• 5．已知P为函数f（x）=lnx+x²图象上一点，则曲线y=f（x）在点P处切线斜率的最小值为（　　）

  A．1

  B． 2

  C． 2 2

  D．4
  组卷：73引用：5难度：0.7

  解析

• 6．数据y与x有较强的线性相关关系，通过计算得到y关于x的线性回归方程为

  ̂

  y

  =

  10

  .

  5

  x

  +

  ̂

  a

  ，经过分析、计算得

  x

  =

  5

  ，

  y

  =

  54

  ，则样本点（6，55）的残差为（　　）

  A．-9.5

  B．9.5

  C．9.6

  D．64.5
  组卷：22引用：2难度：0.6

  解析

• 7．设随机变量X～B（8，

  1

  2

  ），Y=2X-1，则D（Y）=（　　）

  A．1

  B．2

  C．4

  D．8
  组卷：246引用：2难度：0.8

  解析

（二）选考题：共10分.请考生在第22、23题中选一题作答．如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]

• 22．在平面直角坐标系中，曲线C₁的参数方程为

  x = 2 + cosα - sinα

  y = sinα + cosα

  （α为参数），以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，曲线C₂的极坐标方程为

  ρsin

  （

  θ

  +

  π

  4

  ）

  -

  2

  2

  =

  0

  ．
  （1）求曲线C₁的普通方程及曲线C₂的直角坐标方程；
  （2）已知点P（1，0），曲线C₁与曲线C₂交于A，B两点，求

  1

  |

  PA

  |

  +

  1

  |

  PB

  |

  的值．
  组卷：25引用：5难度：0.5

  解析

[选修4-5：不等式选讲]

• 23．已知函数f（x）=2|x|+|2x-1|．
  （1）求不等式f（x）＜3的解集；
  （2）已知函数f（x）的最小值为m,且a,b,c都是正数，a+2b+c=m,证明：

  1

  a

  +

  b

  +

  1

  b

  +

  c

  ≥

  4

  ．
  组卷：16引用：7难度：0.5

  解析