2022-2023学年北京市石景山区华奥学校八年级（下）期末数学试卷

一、选择题（共8小题；共40分）

• 1．下列方程中，关于x的一元二次方程是（　　）

  A．3（x+1）2=2（x+1）	B． 1 x 2 + 1 x - 2 = 0
  C．ax2+bx+c=0	D．x2+2x=x2-1
  组卷：1347引用：13难度：0.9

  解析

• 2．如图将1，

  2

  ，

  3

  ，

  6

  按下列方式排列．若规定（m,n）表示第m排从左向右第n个数，则（5，4）与（15，8）表示的两数之积是（　　）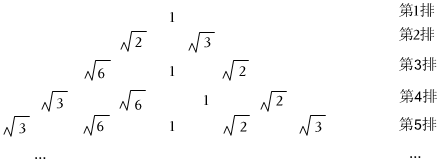
  

  A．1

  B． 2

  C． 6

  D．3 2
  组卷：92引用：1难度：0.5

  解析

• 3．已知四边形ABCD，下列说法正确的是（　　）

  A．当AD=BC，AB∥DC时，四边形ABCD是平行四边形

  B．当AD=BC，AB=DC时，四边形ABCD是平行四边形

  C．当AC=BD，AC⊥BD时，四边形ABCD是正方形

  D．当AC=BD，AC平分BD时，四边形ABCD是矩形
  组卷：196引用：5难度：0.6

  解析

• 4．若点P（-2，3）与点Q（a,b）关于x轴对称，则a,b的值分别是（　　）

  A．-2，3

  B．2，3

  C．-2，-3

  D．2，-3
  组卷：168引用：35难度：0.9

  解析

• 5．若正n边形的每个内角都是120°，则n的值是（　　）

  A．3

  B．4

  C．6

  D．8
  组卷：285引用：11难度：0.9

  解析

• 6．甲、乙两个样本的方差分别是S_甲²=6.06，S_乙²=14.31．由此可反映（　　）

  A．样本甲的波动比样本乙大

  B．样本甲的波动比样本乙小

  C．样本甲和样本乙的波动大小一样

  D．样本甲和样本乙的波动大小关系不能确定
  组卷：58引用：2难度：0.9

  解析

• 7．已知一次函数y=kx-k,若y随x的增大而减小，则该函数的图象经过（　　）

  A．第一，二，三象限	B．第一，二，四象限
  C．第二，三，四象限	D．第一，三，四象限
  组卷：1644引用：72难度：0.7

  解析

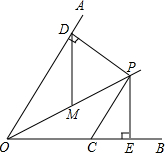• 8．如图，已知OP平分∠AOB，∠AOB=60°，CP=2，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．如果点M是OP的中点，则DM的长是（　　）

  A．2

  B． 2

  C． 3

  D． 2 3
  组卷：2408引用：89难度：0.9

  解析

二、填空题（共6小题；共30分）

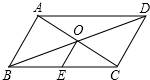• 9．如图，▱ABCD的对角线AC与BD相交于点O，E为BC边中点，已知AB=6cm,则OE的长为

   

  cm.
  组卷：151引用：4难度：0.5

  解析

三、解答题（共13小题；共169分）

• 26．我市某社区今年准备新建一养老中心，其中规划建造三类养老专用房间共100间，这三类养老专用房间分别为单人间（1个养老床位），双人间（2个养老床位），三人间（3个养老床位），因实际需要，单人间房间数在10至30之间（包括10和30），且双人间的房间数是单人间的2倍，设规划建造单人间的房间数为t.
  （Ⅰ）根据题意，填写下表：
  

  单人间的房间数	10	…	t	…	30
  双人间的房间数		…	2t	…	60
  三人间的房间数	70	…		…
  养老床位数	260	…		…

  （Ⅱ）若该养老中心建成后可提供养老床位200个，求t的值；
  （Ⅲ）求该养老中心建成后最多提供养老床位多少个？最少提供养老床位多少个？
  组卷：211引用：2难度：0.3

  解析

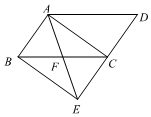• 27．如图，将平行四边形ABCD的边DC延长到点E，使CE=DC，连接AE，交BC于点F，连接AC，BE，若∠AFC=2∠D．求证：四边形ABEC是矩形．
  组卷：477引用：7难度：0.5

  解析