人教新版八年级上册《第11章 三角形》2023年单元测试卷（7）

一、选择题

• 1．下列图形中具有稳定性的是（　　）

  A．平行四边形

  B．长方形

  C．正方形

  D．三角形
  组卷：535引用：20难度：0.7

  解析

• 2．在△ABC中，∠A：∠B：∠C=2：3：4，则△ABC的形状是（　　）

  A．锐角三角形	B．直角三角形
  C．钝角三角形	D．形状无法确定
  组卷：157引用：3难度：0.8

  解析

• 3．已知三角形的两条边长分别为7和3，则第三边的长不能是（　　）

  A．7

  B．6

  C．5

  D．4
  组卷：26引用：2难度：0.9

  解析

• 4．如图，在锐角△ABC中，CD，BE分别是AB，AC边上的高，且CD，BE相交于一点P，若∠A=85°，则∠DPE=（　　）

  A．100°

  B．130°

  C．120°

  D．95°
  组卷：73引用：3难度：0.7

  解析

• 5．如图，在△ABC中，AB=AC，∠A=50°，AB的垂直平分线MN交AC于D点，则∠DBC的度数是（　　）

  A．15°

  B．20°

  C．25°

  D．30°
  组卷：142引用：8难度：0.7

  解析

• 6．小明把一副含45°，30°的直角三角板如图摆放，其中∠C=∠F=90°，∠A=45°，∠D=30°，则∠α+∠β等于（　　）

  A．280°

  B．285°

  C．290°

  D．295°
  组卷：2161引用：11难度：0.7

  解析

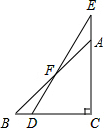• 7．如图，一副分别含有30°和45°角的两个直角三角板，拼成如图所示，其中∠C=90°，∠B=45°，∠E=30°，则∠BFD的度数是（　　）

  A．10°

  B．15°

  C．25°

  D．30°
  组卷：1195引用：20难度：0.7

  解析

• 8．下列说法不正确的是（　　）

  A．在锐角三角形中，最大的锐角x的取值范围是60°≤x＜90°

  B．在△ABC中，锐角的个数最多

  C．在△ABC中三个内角α：β：γ=1：3：5，这个三角形是直角三角形

  D．一个三角形中至少有两个角是锐角
  组卷：137引用：3难度：0.9

  解析

• 9．如图，在△ABC中，∠BAC=90°，AB⊥AC，AB=3，BC=5，EF垂直平分BC，点P为直线EF上的任一点，则AP+BP的最小值是（　　）

  A．4

  B．5

  C．6

  D．7
  组卷：626引用：3难度：0.9

  解析

三、解答题

• 26．如图，已知△ABC的面积是60，请完成下列问题：
  （1）如图1，△ABC中，若AD是BC边上的中线，则△ABD的面积

  △ACD的面积（填“＞”、“＜”或“=”）；
  （2）如图2，若CD、BE分别是△ABC的AB、AC边上的中线，求四边形ADOE的面积可以用如下方法：
  连接AO，由AD=DB得S_△ADO=S_△BDO，
  同理，可得S_△CEO=S_△AEO．
  设S_△ADO=x,S_△AEO=y,则S_△BDO=x,S_△CEO=y.
  由题意得S_△ABE=

  1

  2

  S

  △

  ABC

  =30，S_△ADC=

  1

  2

  S_△ABC=30．
  可列方程组

  2 x + y = 30

  x + 2 y = 30

  ，解得

  ，
  通过解这个方程组可得四边形ADOE的面积为

  ；
  （3）如图3，AD：DB=1：3，CE：AE=2：3，请直接写出四边形ADOE的面积

  .（不用书写过程）
  
  组卷：1283引用：2难度：0.3

  解析

• 27．（1）如图1，AP，BP分别平分∠CAD，∠CBD，则有∠P=

  1

  2

  （∠C+∠D），请说明理由．
  （2）如图2，AP，BP分别平分∠CAD的补角∠CAM和∠CBD．请直接写出∠P与∠C，∠D的关系，不必说明理由．
  组卷：83引用：2难度：0.4

  解析