2022-2023学年海南省洋浦中学高二（下）期中数学试卷

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．已知集合A={（x,y）|x²+y²=1}，B={（x,y）|y=x}，则A∩B中元素的个数为（　　）

  A．3

  B．2

  C．1

  D．0
  组卷：8525引用：37难度：0.9

  解析

• 2．复数

  （

  1

  -

  i

  1

  +

  i

  ）

  2023

  =（　　）

  A．-i

  B．i

  C．-1

  D．1
  组卷：179引用：4难度：0.8

  解析

• 3．等差数列{a_n}的首项为1，公差不为0．若a₂，a₃，a₆成等比数列，则{a_n}前6项的和为（　　）

  A．-24

  B．-3

  C．3

  D．8
  组卷：939引用：23难度：0.7

  解析

• 4．若二项式（

  x

  -

  a

  x

  ）⁶的展开式中常数项为160，则a的值为（　　）

  A．2

  B．-2

  C．4

  D．-4
  组卷：269引用：2难度：0.7

  解析

• 5．用数字0，1，2，3，4，5组成没有重复数字的五位数，其中比40000大的偶数共有（　　）

  A．144个

  B．120个

  C．96个

  D．72个
  组卷：5740引用：35难度：0.9

  解析

• 6．第24届冬季奥林匹克运动会，将于2022年2月在北京和张家口举行，北京冬奥会会徽以汉字“冬”为灵感来源，运用中国书法的艺术形态，将厚重的东方文化底蕴与国际化的现代风格融为一体，呈现出新时代的中国新形象、新梦想．会徽图形上半部分展现滑冰运动员的造型，下半部分表现滑雪运动员的英姿．中间舞动的线条流畅且充满韵律，代表举办地起伏的山峦、赛场、冰雪滑道和节日飘舞的丝带，下部为奥运五环，不仅象征五大洲的团结，而且强调所有参赛运动员应以公正、坦诚的运动员精神在比赛场上相见．其中奥运五环的大小和间距按以下比例（如图）：若圆半径均为12，则相邻圆圆心水平距离为26，两排圆圆心垂直距离为11，设五个圆的圆心分别为O₁，O₂，O₃，O₄，O₅，若双曲线C以O₁，O₃为焦点、以直线O₂O₄为一条渐近线，则C的离心率为（　　）

  A． 290 11

  B． 290 13

  C． 13 11

  D． 12 5
  组卷：122引用：3难度：0.6

  解析

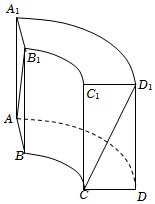• 7．在中国古代数学著作《九章算术》中记载了一种称为“曲池”的几何体，该几何体的上、下底面平行，且均为扇环形（扇环是指圆环被扇形截得的部分）．现有一个如图所示的曲池，它的高为2，AA₁，BB₁，CC₁，DD₁均与曲池的底面垂直，底面扇环对应的两个圆的半径分别为1和2，对应的圆心角为90°，则图中异面直线AB₁与CD₁所成角的余弦值为（　　）

  A． 4 5

  B． 3 5

  C． 3 4

  D． 2 3
  组卷：231引用：12难度：0.6

  解析

四、解答题：本题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤。

• 21．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的离心率为

  1

  2

  ，左、右焦点分别为F₁，F₂，O为坐标原点，点P在椭圆C上，且满足，|PF₂|=2，∠F₁PF₂=

  π

  3

  ．
  （1）求椭圆C的方程；
  （2）已知过点（1，0）且不与坐标轴垂直的直线l与椭圆C交于M，N两点，在x轴上是否存在定点Q，使得∠MQO=∠NQO，若存在，求出点Q的坐标；若不存在，说明理由．
  组卷：64引用：2难度：0.6

  解析

• 22．已知函数f（x）=ae^x-1-lnx+lna.
  （1）当a=e时，求曲线y=f（x）在点（1，f（1））处的切线与两坐标轴围成的三角形的面积；
  （2）若f（x）≥1，求a的取值范围．
  组卷：9334引用：29难度：0.2

  解析