2022-2023学年广东省江门市高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．复数

  z

  =

  7

  +

  i

  1

  -

  i

  的虚部是（　　）

  A．3

  B．4i

  C．4

  D．i
  组卷：58引用：2难度：0.8

  解析

• 2．某小组有1名男生和2名女生，从中任选2名学生参加象棋比赛，事件“至多有1名男生”与事件“至多有1名女生”是（　　）

  A．对立事件	B．必然事件
  C．互斥事件	D．相互独立事件
  组卷：143引用：2难度：0.7

  解析

• 3．小红参加学校举行的演讲比赛，6位评委对她的评分如下：82，78，85，81，90，88，若选手的最终得分计算需要去掉一个最低分和一个最高分，则小红的最终得分的平均数和方差分别为（　　）

  A．83，6.5

  B．87，8.5

  C．83，9.5

  D．84，7.5
  组卷：99引用：2难度：0.9

  解析

• 4．已知

  a

  =

  （

  2

  ，

  1

  ）

  ，

  b

  =

  （

  -

  3

  ，

  4

  ）

  ，则向量

  a

  在向量

  b

  上的投影向量为（　　）

  A． （ 6 5 ，- 8 5 ）

  B． （ 6 25 ，- 8 25 ）

  C． （ - 6 5 ， 8 5 ）

  D． （ - 6 25 ， 8 25 ）
  组卷：139引用：2难度：0.5

  解析

• 5．在△ABC中，

  cos

  A

  =

  3

  5

  ，tanB=2，则tan（A+B）=（　　）

  A．2

  B． 5 3

  C．-2

  D． - 5 3
  组卷：118引用：4难度：0.7

  解析

• 6．已知圆锥的表面积为27π，且它的侧面展开图是一个半圆，则圆锥底面直径为（　　）

  A．6

  B．3

  C．12

  D． 3 3
  组卷：138引用：2难度：0.8

  解析

• 7．在△ABC中，内角A，B，C所对的边分别为a,b,c,且若a²+c²+ac=b²，外接圆的半径为1，则△ABC面积的最大值为（　　）

  A． 3 4

  B． 3 4

  C． 3 2

  D． 3 3 4
  组卷：187引用：4难度：0.6

  解析

四、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．

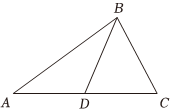• 21．在△ABC中，a,b,c分别是角A，B，C所对的边，

  B

  =

  π

  3

  ，b=6，sinC=3sinA．
  （1）求△ABC的面积；
  （2）若D为AC的中点，求BD的长．
  组卷：115引用：2难度：0.6

  解析

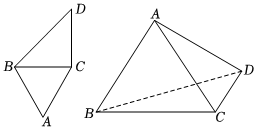• 22．如图，ABDC是平面四边形，△ABC为正三角形，BC=CD=4，BC⊥CD．将△ABC沿BC翻折，过点A作平面BCD的垂线，垂足为H．
  （1）若点H在线段BD上，求AD的长；
  （2）若点H在BCD内部，且直线AB与平面ACD所成角的正弦值为

  3

  13

  13

  ，求二面角A-BC-D的余弦值．
  组卷：204引用：4难度：0.4

  解析