2022-2023学年江苏省连云港市高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．

  1

  +

  i

  1

  -

  i

  的值为（　　）

  A．1

  B．-1

  C．i

  D．-i
  组卷：140引用：11难度：0.9

  解析

• 2．甲、乙、丙三人在3天节日中值班，每人值班1天，则甲紧接着排在乙的前面值班的概率是（　　）

  A． 1 6

  B． 1 4

  C． 1 3

  D． 1 2
  组卷：129引用：11难度：0.9

  解析

• 3．设

  a

  ，

  b

  是单位向量，若

  a

  ⊥

  b

  ，则

  （

  a

  +

  b

  ）

  •

  b

  的值为（　　）

  A．1

  B．0

  C．-1

  D． - 2
  组卷：83引用：5难度：0.8

  解析

• 4．为激发中学生对天文学的兴趣，某校举办了“2022～2023学年中学生天文知识竞赛”，并随机抽取了200名学生进行成绩统计，发现抽取的学生的成绩都在50分至100分之间，进行适当分组后（每组为左闭右开的区间），画出频率分布直方图如图所示，下列说法正确的是（　　）

  A．直方图中x的值为0.035

  B．估计全校学生的平均成绩不低于80分

  C．估计全校学生成绩的样本数据的60百分位数约为60分

  D．在被抽取的学生中，成绩在区间[60，70）的学生数为10
  组卷：59引用：2难度：0.7

  解析

• 5．若sinαtanα=cosα-5sinα，则cos4α=（　　）

  A． - 21 29

  B． - 1 9

  C． 1 9

  D． 21 29
  组卷：166引用：2难度：0.7

  解析

• 6．在长方体ABCD-A₁B₁C₁D₁中，已知

  AB

  =

  AD

  =

  3

  ，AA₁=1，则A₁B和AD₁所成角的余弦值为（　　）

  A． 1 3

  B． 1 4

  C． 1 5

  D． 1 6
  组卷：143引用：1难度：0.8

  解析

• 7．四名同学各掷骰子5次，分别记录每次骰子出现的点数，根据四名同学的统计结果，可以判断出一定没有出现点数5的是（　　）

  A．平均数为3，中位数为2	B．中位数为3，众数为2
  C．中位数为3，方差为1.2	D．平均数为2，方差为1.6
  组卷：43引用：1难度：0.7

  解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

• 21．已知函数

  f

  （

  x

  ）

  =

  co

  s

  2

  x

  +

  2

  3

  sinxcosx

  -

  si

  n

  2

  x

  +

  m

  的最大值为1．
  （1）求常数m的值；
  （2）若

  f

  （

  x

  0

  2

  ）

  =

  1

  5

  ，

  x

  0

  ∈

  [

  0

  ，

  π

  3

  ]

  ，求cos2x₀的值．
  组卷：135引用：4难度：0.5

  解析

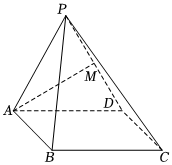• 22．如图，在四棱锥P-ABCD中，底面ABCD为矩形，侧面PAD是边长为2的正三角形，CD⊥平面PAD，M是PD的中点．
  （1）证明：AM⊥PC；
  （2）若直线PC与平面ABCD所成角的正切值为

  3

  2

  ，求侧面PAD与侧面PBC所成二面角的大小．
  组卷：99引用：1难度：0.6

  解析