2022-2023学年北京市昌平实验学校高二（上）期中数学试卷

一、选择题（每题4分）

• 1．设i为虚数单位，复数z₁=1-3i,z₂=3-2i,则z₁-z₂在复平面内对应的点在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：5引用：2难度：0.9

  解析

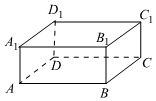• 2．如图，在长方体ABCD-A₁B₁C₁D₁中，化简

  AB

  -

  AD

  +

  C

  C

  1

  =（　　）

  A． D B 1

  B． B D 1

  C． A C 1

  D． A 1 C
  组卷：137引用：8难度：0.9

  解析

• 3．已知l是直线，α、β是两个不同平面，下列命题中的真命题是（　　）

  A．若l∥α，l∥β，则α∥β	B．若α⊥β，l∥α，则l⊥β
  C．若l⊥α，l∥β，则α⊥β	D．若l∥α，α∥β，则l∥β
  组卷：273引用：13难度：0.9

  解析

• 4．设A（3，2，1），B（1，0，5），则AB的中点M的坐标为（　　）

  A．（-2，-2，4）

  B．（-1，-1，2）

  C．（2，1，3）

  D．（4，2，6）
  组卷：525引用：4难度：0.8

  解析

• 5．直线

  3

  x

  -

  y

  +

  2

  =

  0

  的倾斜角为（　　）

  A．30°

  B．60°

  C．120°

  D．150°
  组卷：360引用：32难度：0.9

  解析

• 6．已知直线l经过点P（-1，3），且与直线x-2y+3=0平行，则直线l的方程为（　　）

  A．x-2y-5=0

  B．2x+y-1=0

  C．x-2y+7=0

  D．2x+y-5=0
  组卷：123引用：8难度：0.8

  解析

• 7．直线y=x与直线y=x+1间的距离等于（　　）

  A． 1 2

  B． 2 2

  C．1

  D． 2
  组卷：222引用：2难度：0.8

  解析

三、解答题（16-17每题13分，18题14分，19-21每题15分）

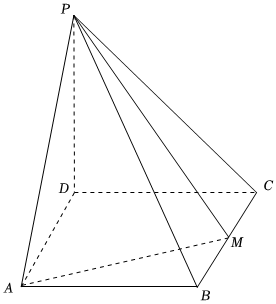• 20．如图，四棱锥P-ABCD的底面是矩形，PD⊥底面ABCD，PD=DC=1，AD=2，M为BC的中点．
  （1）求证：AD⊥PC．
  （2）求直线PB与平面PAM所成角的正弦值．
  （3）求平面PAM与平面PCD的夹角的余弦值．
  组卷：63引用：3难度：0.4

  解析

• 21．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的一个顶点为P（0，1），且离心率为

  3

  2

  ．
  （1）求椭圆C的方程；
  （2）已知点Q坐标为（-2，0），直线y=2x+1与椭圆C交于A、B两点，求△ABQ的面积；
  （3）若直线l：y=x+m与椭圆C交于M、N两点，且|PM|=|PN|，求m的值．
  组卷：25引用：2难度：0.5

  解析